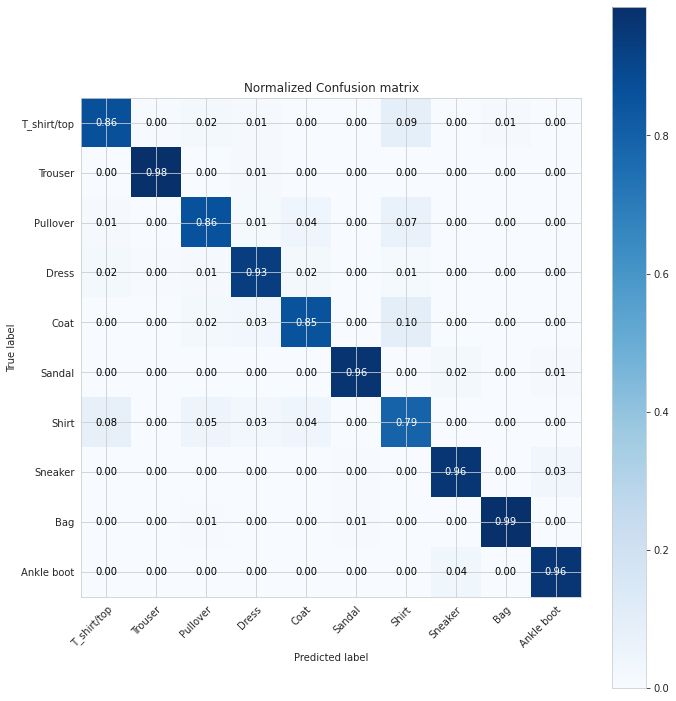
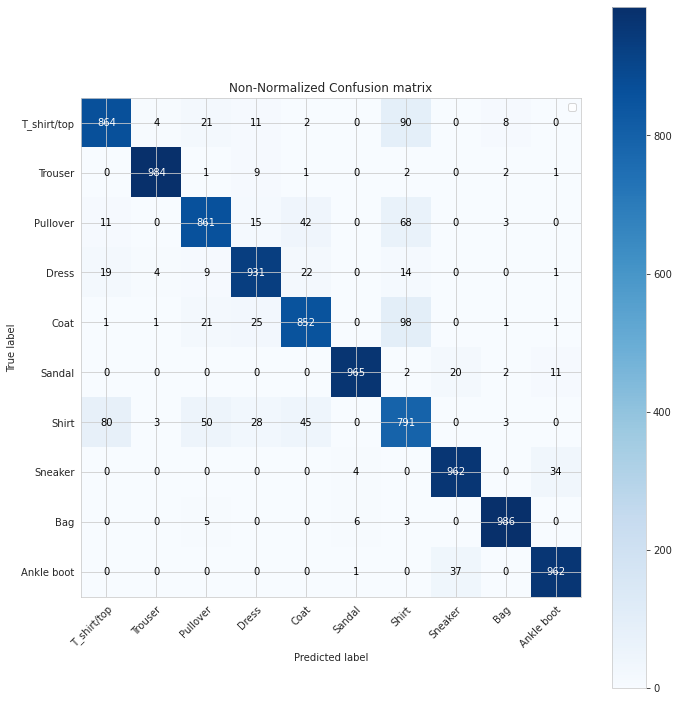
La moltiplicazione di matrici è tra le operazioni più fondamentali e ad alta intensità di calcolo nell’apprendimento automatico.
“La moltiplicazione della matrice è tra le operazioni più fondamentali e ad alta intensità di calcolo nell’apprendimento automatico.”
Le operazioni fondamentali di qualsiasi tipica rete neurale possono essere ridotte a un mucchio di operazioni di addizione e moltiplicazione. Le reti neurali possono essere espresse in termini di matrici. La moltiplicazione di matrici è una delle operazioni matematiche più importanti quando si tratta di reti neurali profonde. Che si tratti di un’operazione di convoluzione di una CNN per riconoscere le immagini o di un modello linguistico per eseguire l’analisi del sentimento; queste operazioni aritmetiche di base svolgono un ruolo enorme. Anche i moderni set di dati di grandi dimensioni sono spesso espressi come matrici di grandi dimensioni. Ad esempio, nel modello bag-of-words, ogni riga della matrice corrisponde a un documento. Mentre, nel caso dell’analisi delle immagini, i valori delle caratteristiche sono rappresentati da una matrice con righe corrispondenti alle immagini. Anche le TPU di Googlesono definiti in termini di matrici. Le TPU hanno tensori, che sono array o matrici multidimensionali. Le operazioni matematiche di base eseguite sui tensori, tra cui addizione, moltiplicazione per elemento e moltiplicazione di matrici, sono inseparabili dal mondo del deep learning.
Emozionanti ricerche sull’intelligenza artificiale a cui guardare nel 2020
I ricercatori di Stanford risolvono una cosa che ha infastidito i droni
Hugging Face lancia Optimum, un toolkit di ottimizzazione open source per trasformatori su larga scala
Come viene utilizzata la trasformata di Fourier nel deep learning?
Una guida per principianti ai TPU
Poiché la moltiplicazione della matrice è uno dei processi fondamentali di una rete neurale profonda, qualsiasi possibilità di accelerare questo processo può ridurre i lunghi tempi di addestramento, di cui di solito vengono attribuiti i DNN. I precedenti lavori mirati ad accelerare il deep learning hanno sviluppato librerie di moltiplicazione di matrici ad alta velocità, progettato hardware personalizzato per accelerare la moltiplicazione di matrici e progettato algoritmi efficienti di moltiplicazione approssimativa della matrice (AMM) in base a vari presupposti. AMM, secondo Ye et al., rende il calcolo matriciale adatto per set di dati su larga scala.
Recentemente, i ricercatori Davis Blalock e John Guttag hanno introdotto un algoritmo basato sull’apprendimento per questo compito che supera di gran lunga i metodi esistenti. Questo metodo si discosta dall’approccio AMM esistente in quanto si basa sull’hashing e sulle ricerche nelle tabelle anziché sulle operazioni di aggiunta multipla.
I metodi esistenti cercano di ridurre al minimo il tempo di calcolo approssimando le operazioni lineari. Questa sfida di solito sorge nell’apprendimento automatico quando si ha una matrice di dati, ad esempio A, le cui righe sono campioni, e un operatore lineare, ad esempio B, che potrebbe anche essere un classificatore lineare, un regressore o una matrice di incorporamento. Questo nuovo metodo di Blalock e Guttag, noto come PAZZA, utilizza una funzione di preelaborazione non lineare e riduce il problema alle ricerche nelle tabelle.
Se l’applicazione di un modello lineare addestrato a nuovi dati porta alla conoscenza dell’operatore lineare, l’algoritmo MADDNESS non richiede operazioni di moltiplicazione. “Il nostro metodo è più strettamente correlato ai metodi di quantizzazione vettoriale utilizzati per la ricerca di similarità. Tuttavia, invece di utilizzare una costosa funzione di quantizzazione che richiede molte moltiplicazioni, introduciamo una famiglia di funzioni di quantizzazione che non richiedono moltiplicazioni”, hanno affermato i ricercatori nel loro recente lavoro , presentato alla conferenza ICML 2021. Il metodo di quantizzazione, che è la chiave di questo algoritmo, si riferisce a un classico algoritmo di quantizzazione vettoriale utilizzato per approssimare prodotti interni ed euclidei.
Per valutare l’efficacia di MADDNESS, i ricercatori hanno implementato il loro metodo e gli algoritmi esistenti in C++ e Python utilizzando un singolo thread su un Macbook Pro con un processore Intel Core i7-4960HQ a 2,6GHz. Per quanto riguarda l’uso di CPU al posto delle GPU, gli autori hanno affermato che i modelli ML addestrati sono comunemente distribuiti su miliardi di smartphone con solo CPU. Ciò ha simulato uno scenario del mondo reale, rendendo anche più facile per i ricercatori in futuro confrontare il proprio lavoro senza la necessità di una costosa configurazione della GPU.
Nel convalidare il metodo MADDNESS su centinaia di matrici di domini diversi, Blalock e Guttag hanno osservato che il loro metodo “spesso” funziona 100 volte più velocemente dei prodotti di matrici esatte e 10 volte più velocemente degli attuali metodi approssimati.
Detto questo, gli autori ammettono anche che il loro metodo non sarà all’altezza se applicato su algoritmi all’avanguardia poiché le operazioni di convoluzione per i modelli SOTA sfruttano la struttura che non è disponibile per gli algoritmi di moltiplicazione di matrici generali. Per abbinare le prestazioni, è necessario apportare modifiche all’approccio PAZZA. Tuttavia, Blalock e Guttag ritengono che il loro metodo possa ispirare altre ricerche che alla fine possono portare all’accelerazione delle operazioni di convoluzione e ad altri carichi di lavoro ostacolati dalle trasformazioni lineari.