Le reti neurali possono svolgere bene compiti come la classificazione delle immagini, la traduzione della lingua e il gioco. Tuttavia, di solito non riescono a svolgere bene i compiti che richiedono astrazione umana. Attività come la cattura di palle a mezz’aria o la giocoleria di più palle, che gli umani hanno imparato, hanno bisogno di una comprensione intuitiva della dinamica di come si comportano i corpi fisici.
Non ci prendiamo del tempo per calcolare le traiettorie prima di colpire la palla. Lo sappiamo e basta.
I modelli di apprendimento automatico mancano di molte intuizioni di base sulle dinamiche del mondo fisico. Una rete neurale non può mai afferrare l’astrazione a livello umano, anche dopo aver visto migliaia di esempi.
IL PROBLEMA DI BASE CON I MODELLI DI RETI NEURALI È CHE FANNO FATICA A IMPARARE LE SIMMETRIE DI BASE E LE LEGGI SULLA CONSERVAZIONE
Una soluzione a questo problema è progettare reti neurali in grado di apprendere leggi di conservazione arbitrarie.
Sam Greydanus , residente a Google Brain, insieme ai suoi colleghi, Miles Cranmer, Peter Battaglia, David Spergel, Shirley Ho e Stephen Hoyer ha pubblicato un interessante documento che affronta le sfide di cui sopra. Nella prossima sezione parleremo brevemente delle reti neurali lagrangiane e del perché siano significative
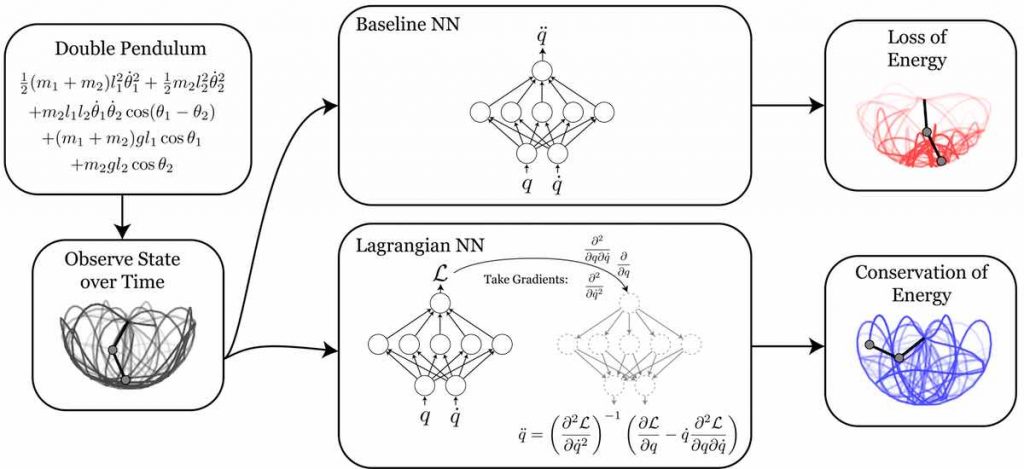
Panoramica delle reti neurali lagrangiane
Un doppio pendolo
Per dimostrare come un lagrangiano denoti i segreti sottostanti della natura, gli autori prendono l’esempio di un doppio pendolo. Un doppio pendolo è un pendolo attaccato ad un pendolo. È famoso per rappresentare il caos nei corpi in movimento.
Considera un sistema fisico con coordinate x_t = (q, q˙). Ad esempio, un doppio pendolo può essere definito con l’aiuto degli angoli che crea e anche delle sue velocità angolari.
Quando un doppio pendolo viene messo in movimento, le coordinate che abbiamo attribuito al corpo si spostano da un punto all’altro. Questo è chiaro Questo è buon senso.
Ma ciò che induce il caos è la possibilità di molti percorsi che queste coordinate possono prendere tra inizio (x_0) e fine (x_1).
Secondo la meccanica lagrangiana, qualsiasi azione può essere scritta in funzione dell’energia potenziale (energia in virtù della posizione) e dell’energia cinetica (in virtù del movimento). E, è espresso come segue:
La S nell’espressione sopra ha una proprietà notevole. Per tutti i possibili percorsi tra x_0 e x_1, esiste un solo percorso, che fornisce un valore stazionario di S. Inoltre, quel percorso è quello che la natura prende sempre – il principio della minima azione.
Quindi, se comprendiamo le leggi di conservazione dell’energia, allora possiamo definire l’azione del corpo in esame e infine prevedere il percorso intrapreso dal corpo con grande precisione.
Tuttavia, le reti neurali sono scarse nel comprendere la perdita di concetti energetici, ed è qui che entrano in gioco le reti neurali di Lagrangian (LNN).
“SE L’ENERGIA VIENE PRESERVATA”, POTREBBERO DIRE, “QUANDO LANCIO UNA PALLA VERSO L’ALTO, TORNERÀ ALLA MIA MANO CON LA STESSA VELOCITÀ DI QUANDO È PARTITA.”
tramite il blog di Sam Greydanus
Ma queste regole di buon senso possono essere difficili da imparare direttamente dai dati. Quindi, una rete neurale che comprende la conservazione dell’energia solo dai dati può avere grandi implicazioni per la robotica e l’apprendimento per rinforzo. E, con le LNN, gli autori hanno aperto nuove strade di ricerca vincolando i principi di base della natura con le reti neurali artificiali create dall’uomo.
Qual è il significato degli LNN
Un francobollo francese che commemora Lagrange
Joseph-Louis Lagrange, nato nel 1736, in Italia, è uno dei più grandi polimeri che siano mai vissuti. A 20 anni ha già pubblicato il principio della minima azione nella dinamica dei corpi solidi e fluidi. Ha formulato come trovare il percorso seguito dai corpi, non importa quanto caotici siano i loro movimenti. Tre secoli dopo, oggi, il suo lavoro risuona ancora nei campi più avanzati come il deep learning.
Non che ci sia una data di scadenza per i fondamenti della matematica, ma il fatto che quei principi possano essere applicati per rendere le reti neurali migliori di prima è un’idea affascinante.
I modelli dell’universo vengono analizzati per le loro simmetrie durante la formulazione di un modello. Queste simmetrie corrispondono alle leggi di conservazione dell’energia e della quantità di moto, che la rete neurale lotta per l’apprendimento.
Per ovviare a queste carenze, lo scorso anno Greydanus e i suoi colleghi hanno introdotto una classe di modelli chiamati Hamiltonian Neural Networks (HNN), che possono apprendere queste quantità invarianti direttamente dai dati (pixel). Ora, facendo un passo avanti rispetto agli HNN, le reti neurali di Lagrangian (LNN) possono apprendere le funzioni lagrangiane direttamente dai dati. Questo può essere fatto anche dagli HNN, ma a differenza degli HNN non richiedono coordinate canoniche.
La tabella sopra mette gli LNN contro altri lavori correlati e possiamo vedere chiaramente che le reti neurali lagrangiane stanno vincendo e dobbiamo aspettare e vedere quali altri progressi hanno in serbo per la comunità scientifica.