“La doppia discesa non avviene attraverso la profondità.”
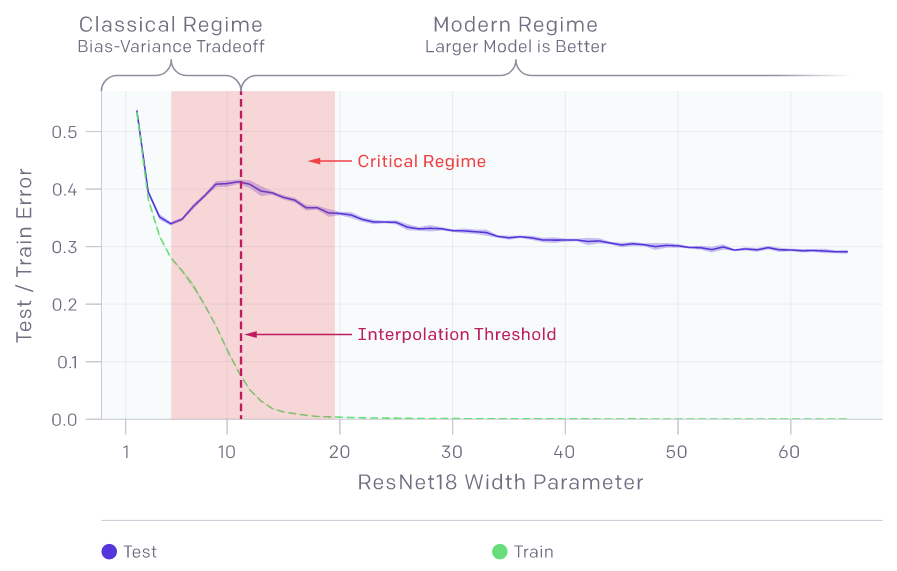
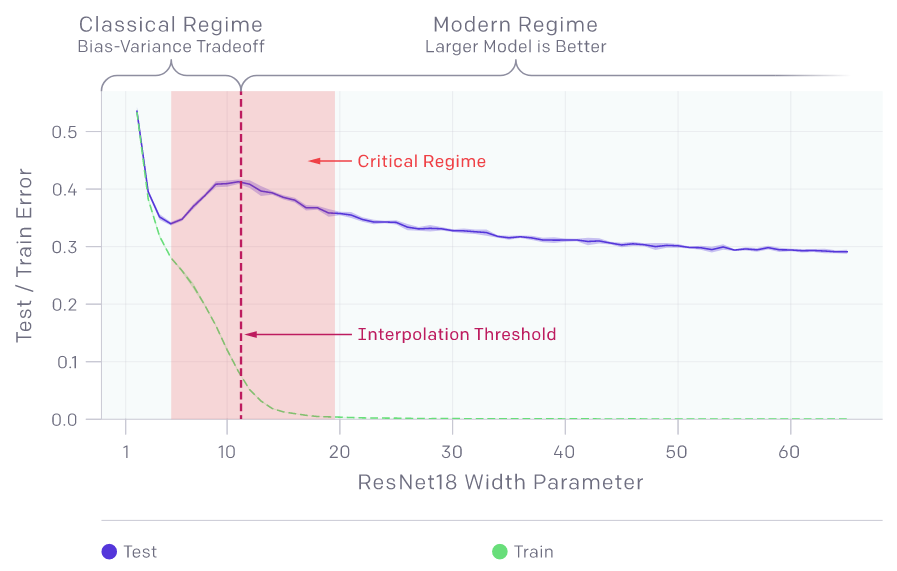
La curva a doppia discesa indica che l’aumento della capacità del modello oltre la soglia di interpolazione può portare a una diminuzione dell’errore di test. L’aumento della capacità della rete neurale attraverso la larghezza porta a una doppia discesa . Ma per quanto riguarda la profondità della rete neurale? Come si gioca l’aumento o la riduzione della profondità verso la fine? Un gruppo di ricercatori del MIT ha tentato di esplorare questa domanda nel loro lavoro intitolato ” Do Deeper Convolutional Networks Perform Better? “.
La profondità e la morte della complessità
Illustrazione della doppia discesa. (Fonte: OpenAI)
Non aderendo alla nozione comune che la teoria dell’apprendimento automatico statistico standard prevede che i modelli più grandi dovrebbero essere più inclini all’overfitting , Mikhail Belkin e i suoi colleghi nel loro articolo fondamentale hanno scoperto che il compromesso standard bias-varianza deraglia effettivamente una volta raggiunta la “soglia di interpolazione “.
Le statistiche ci dicono che la parametrizzazione eccessiva porta all’overfitting. Cioè, man mano che i modelli diventano complessi, la loro capacità di generalizzare diminuisce. Le reti neurali profonde, al contrario, hanno funzionato bene con l’aumentare della complessità. Il fenomeno chiamato doppia discesa, spiega questo enigma. Prima di addentrarci ulteriormente nella profondità di una rete e di una doppia discesa, discutiamo brevemente della doppia discesa stessa. Il concetto di doppia discesa è stato reso popolare alla fine dell’anno scorso dai ricercatori di OpenAI .
I ricercatori di OpenAI hanno esplorato il compromesso bias-varianza prima che si mantenga la soglia di interpolazione e come la crescente complessità del modello porti a un overfitting, aumentando l’errore di test. La doppia discesa ha introdotto il concetto di soglia di interpolazione e il modo in cui i risultati variano a seconda del lato della soglia su cui si trovano e una volta superata questa soglia, l’errore di test si riduce.
Il lavoro presenta due situazioni in cui l’errore del test aumenta con la dimensione del campione:
(A): l’errore di addestramento aumenta con la dimensione del campione
(B): il divario di generalizzazione aumenta con la dimensione del campione.
Ora possono esistere casi in cui (A) è vero e (B) è falso e viceversa o dove entrambi (A) e (B) sono veri.
I modelli per un numero critico di campioni, si sforzano di adattarsi al set del treno. Ciò può distruggere la struttura globale del modello. Per un numero inferiore di campioni, i ricercatori di OpenAI hanno affermato che i modelli sono sufficientemente parametrizzati da adattarsi al set di treni mentre si comportano ancora bene sulla distribuzione.
Fino allo scorso anno il comportamento in doppia discesa non era stato esplorato a causa di diversi ostacoli. La curva a doppia discesa, per essere osservata, richiede una famiglia parametrica di spazi con funzioni di complessità arbitraria.
Finora, la complessità è definita in termini di aumento della larghezza della rete. Allora, che ruolo ha la profondità?
{Nota: una larghezza è un numero di nodi su ogni livello mentre la profondità è il numero di livelli stessi.}
Per comprendere il ruolo della profondità, i ricercatori del MIT hanno considerato le reti neurali lineari. Secondo gli autori, le reti neurali lineari sono utili per analizzare i fenomeni di deep learning poiché rappresentano operatori lineari ma hanno paesaggi di ottimizzazione non convessi. Inoltre, la soluzione appresa da una rete completamente connessa a livello singolo è ben compresa.
Gli esperimenti sugli autoencoder lineari e sui classificatori convoluzionali lineari, hanno concluso gli autori, dimostrano costantemente che l’accuratezza del test diminuisce una volta raggiunta la soglia di interpolazione.
Takeaway chiave
Esperimenti nell’impostazione di classificazione su CIFAR10 e ImageNet32 utilizzando ResNets e reti completamente convoluzionali dimostrano che le prestazioni dei test peggiorano oltre una profondità critica.
L’accuratezza del test delle reti convoluzionali si avvicina a quella delle reti completamente connesse all’aumentare della profondità.
L’aumento della profondità porta a una scarsa generalizzazione.
Contro la saggezza convenzionale, i nostri risultati indicano che quando i modelli sono vicini o superano la soglia di interpolazione (ad esempio, raggiungendo una precisione di allenamento del 100%), i professionisti dovrebbero diminuire la profondità di queste reti per migliorare le loro prestazioni.
La forza trainante del successo del deep learning non è la profondità dei modelli, ma piuttosto la loro ampiezza.