Esistono molte applicazioni aziendali di previsione di serie storiche come la previsione del prezzo delle azioni, le previsioni di vendita, le previsioni meteorologiche ecc. In questa attività di previsione delle serie temporali vengono applicati numerosi modelli di apprendimento automatico. Ogni modello ha i suoi vantaggi e svantaggi. In questo articolo, vedremo un confronto tra due modelli di previsione di serie storiche: il modello ARIMA e il modello LSTM RNN. Entrambi questi modelli sono applicati nella previsione del prezzo delle azioni per vedere il confronto tra di loro.
Modello ARIMA
Il modello ARIMA, o modello di media mobile integrata auto-regressiva, è adattato ai dati delle serie temporali per analizzare i dati o per prevedere i punti di dati futuri su una scala temporale. Il più grande vantaggio di questo modello è che può essere applicato nei casi in cui i dati mostrano prove di non stazionarietà.
L’auto-regressivo significa che la variabile di interesse in evoluzione viene regredita sul proprio valore precedente e la media mobile indica che l’errore di regressione è in realtà una combinazione lineare di termini di errore i cui valori si sono verificati contemporaneamente e in varie occasioni nel passato. Il significato dell’integrazione nel modello ARIMA è che i valori dei dati sono stati sostituiti con la differenza tra i loro valori e i valori precedenti
Per maggiori dettagli sull’analisi delle serie storiche utilizzando il modello ARIMA, consultare i seguenti articoli: –
Una guida introduttiva alla previsione di serie storiche
Modellazione di serie storiche e prove di stress – Utilizzo di ARIMAX
Rete neurale ricorrente LSTM
Le reti neurali ricorrenti con memoria LSTM o memoria a breve termine sono le varianti delle reti neurali artificiali. A differenza delle reti feedforward in cui i segnali viaggiano solo in avanti, in LSTM RNN, i segnali di dati viaggiano in direzioni arretrate e queste reti hanno connessioni di feedback. LSTM RNN viene comunemente utilizzato nelle previsioni delle serie temporali. Per maggiori dettagli su questo modello, consultare i seguenti articoli: –
Come codificare la tua prima rete LSTM in Keras
Guida pratica alla rete neurale ricorrente LSTM per la previsione del mercato azionario.
Ora vedremo un confronto delle previsioni di entrambi i modelli sopra. Per l’implementazione, abbiamo utilizzato i prezzi storici delle azioni per addestrare e testare i nostri modelli. I valori storici degli stock vengono scaricati da nsepy che è un’API python.
Implementazione della previsione di serie storiche
Prima di tutto, dobbiamo importare tutte le librerie richieste. nsepy deve essere installato usando ‘ pip install nsepy ‘ prima di importarlo qui. Per utilizzare il modello LSTM, è necessario installare TensorFlow poiché viene applicato il backend TensorFlow per il modello LSTM. Il pmdarima deve anche essere installato usando ‘ pip install pmdarima ‘ per usare il modello ARIMA.
Importing di librerie
da nsepy get_history importazione come gh
datetime import come dt
da matplotlib importazione pyplot come PLT
da sklearn importazione model_selection
da sklearn.metrics importano confusion_matrix
da sklearn.preprocessing importazione StandardScaler
da sklearn.model_selection importazione train_test_split
importazione NumPy come np
panda di importazione come pd
da sklearn.preprocessing import MinMaxScaler
da keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
da keras.layers import Dropout
from pmdarima import auto_arima
import
alert from statsmodels.tsa.seasonal season_decompose
da statsmodels.tsa.statespace.sarimax import SARIMAX
Una volta installate le librerie, dobbiamo recuperare i dati passando la data di inizio e la data di fine alla funzione API. Successivamente i dati scaricati verranno preelaborati.
Impostazione delle date di inizio e fine e recupero dei dati storici
start = dt.datetime (2013,1,1)
end = dt.datetime (2019,12,31)
stk_data = gh (symbol = ‘SBIN’, start = start, end = fine)
Data Preelaborazione
stk_data [‘Date’] = stk_data.index
data2 = pd.DataFrame (colonne = [‘Data’, ‘Apri’, ‘Alto’, ‘Basso’, ‘Chiudi’])
data2 [‘Data’] = stk_data [‘Date’]
data2 [‘Open’] = stk_data [‘Open’]
data2 [‘High’] = stk_data [‘High’]
data2 [‘Low’] = stk_data [‘Low’]
data2 [‘Chiudi’ ] = stk_data [‘Chiudi’]
Quando saremo pronti con il set di dati, inseriremo il modello ARIMA utilizzando lo snippet di codice seguente e tracciamo il risultato.
############### ARIMA ############################ ###
Ignora avvisi innocui
warnings.filterwarnings (“ignore”)
Adatta la funzione auto_arima ai dati di borsa
stepwise_fit = auto_arima (data2 [‘Chiudi’], start_p = 1, start_q = 1, max_p = 3, max_q = 3, m = 12, start_P = 0, stagionale = True, d = None , D = 1, trace = True, error_action = ‘ignore’, suppress_warnings = True, stepwise = True)
Per stampare il riepilogo
stepwise_fit.summary ()
Dividi i dati in treno / set di test
train = data2.iloc [: len (data2) -150]
test = data2.iloc [len (data2) -150:]
Adatta un
modello SARIMAX = SARIMAX (data2 [‘Close’], order = (0, 1, 1), seasonal_order = (2, 1, 1, 12))
result = model.fit ()
result.summary ()
inizio = len (treno)
fine = len (treno) + len (test) – 1
Pronostici per un anno rispetto alle
previsioni del set di test = risultato.predetto (inizio, fine, tipo = ‘livelli’). Rinomina (“Pronostici”)
previsioni della trama e valori effettivi
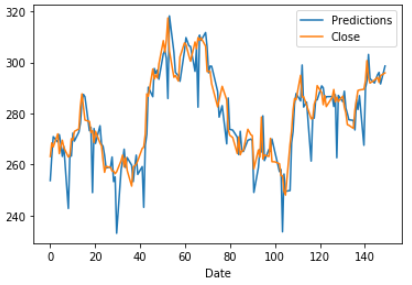
predictions.plot (legenda = Vero)
test [‘Chiudi’]. plot (legenda = Vero)
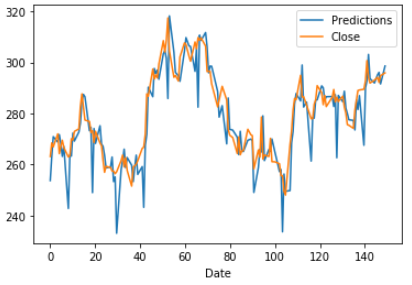
Dopo aver visualizzato il grafico delle serie temporali utilizzando il modello ARIMA, vedremo la stessa analisi per modello LSTM.
#######
LSTM
######################### train_set = data2.iloc [0: 1333 :, 1 : 2] .values sc = MinMaxScaler (feature_range = (0, 1))
training_set_scaled = sc.fit_transform (train_set)
X_train = []
y_train = []
per i nell’intervallo (60, 1333):
X_train.append (training_set_scaled [i -60: i, 0])
y_train.append (training_set_scaled [i, 0])
X_train, y_train = np.array (X_train), np.array (y_train)
X_train = np.reshape (X_train, (X_train.shape [0 ], X_train.shape [1], 1))
Definizione del
regressore
modello ricorrente LSTM = regressore sequenziale () regressor.add (LSTM (unità = 50, return_sequences = True, input_shape = (X_train.shape [1], 1)))
regressor.add (Dropout (0.2))
. add (LSTM (unità = 50, return_sequences = True))
regressor.add (Dropout (0.2))
regressor.add (LSTM (unità = 50, return_sequences = True))
regressor.add (Dropout (0.2))
regressor.add ( LSTM (unità = 50))
regressor.add (Dropout (0.2))
regressor.add (Denso (unità = 1))
Compilazione e adattamento del modello
regressor.compile (optimizer = ‘adam’, loss = ‘mean_squared_error’)
regressor.fit (X_train, y_train, epochs = 15, batch_size = 32)
Recupero dei dati di test e preelaborazione
testdataframe = gh (symbol = ‘SBIN’, start = dt.datetime (2018,5,23), end = dt.datetime (2018,12,31))
testdataframe [‘Date’] = testdataframe.index
testdata = pd.DataFrame (colonne = [‘Data’, ‘Apri’, ‘Alto’, ‘Basso’, ‘Chiudi’])
testdata [‘Data’] = testdataframe [‘Data’]
testdata [‘Apri ‘] = testdataframe [‘ Open ‘]
testdata [‘ High ‘] = testdataframe [‘ High ‘]
testdata [‘ Low ‘] = testdataframe [‘ Low ‘]
testdata [‘ Close ‘] = testdataframe [‘ Close ‘]
real_stock_price = testdata.iloc [:, 1: 2] .values
dataset_total = pd.concat ((data2 [‘Open’], testdata [‘Open’]),axis = 0)
input = dataset_total [len (dataset_total) – len (testdata) – 60:]. valori
input = inputs.reshape (-1,1)
input = sc.transform (input)
X_test = []
per i nell’intervallo (60, 235):
X_test.append (input [i-60: i, 0])
X_test = np.array (X_test)
X_test = np.reshape (X_test, (X_test.shape [0], X_test.shape [1], 1))
Fare previsioni sui dati del test
predicted_stock_price = regressor.predict (X_test)
predicted_stock_price = sc.inverse_transform (predicted_stock_price)
Visualizzare la previsione
plt.figure ()
plt.plot (real_stock_price, color = ‘r’, label = ‘Close’)
plt.plot (predicted_stock_price, color = ‘b’, label = ‘Prediction’)
plt.xlabel (‘ Data “)
plt.legend ()
plt.show ()
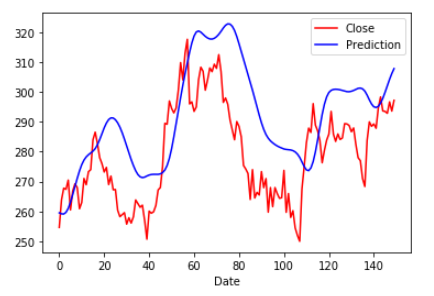
modello lstm
Confrontando i due grafici di previsione, possiamo vedere che il modello ARIMA ha previsto prezzi di chiusura molto più bassi dei prezzi reali. Questa grande variazione nella previsione può essere vista nella maggior parte dei punti della trama. Ma nel caso del modello LSTM, la stessa previsione dei prezzi di chiusura può essere vista superiore al valore reale. Ma questa variazione può essere osservata in alcuni punti della trama e la maggior parte delle volte, il valore previsto sembra essere vicino al valore reale. Quindi possiamo concludere che, nel compito di previsione delle scorte, il modello LSTM ha sovraperformato il modello ARIMA.
Infine, per maggiore soddisfazione, proveremo a scoprire l’errore quadratico medio di radice (RMSE) nella previsione di entrambi i modelli.
RMSE #######
da sklearn.metrics import mean_squared_error
da statsmodels.tools.eval_measures import rmse
RMSE per il modello ARIMA
err_ARIMA = rmse (test [“Chiudi”], previsioni)
print (‘RMSE con ARIMA’, err_ARIMA)
RMSE per modello
LSTM err_LSTM = rmse (test [“Chiudi”], predicted_stock_price)
print (‘RMSE con LSTM’, err_LSTM)
RMSE
Vedendo gli RMSEs, è chiaro ora che il modello LSTM ha le migliori prestazioni in questo compito.