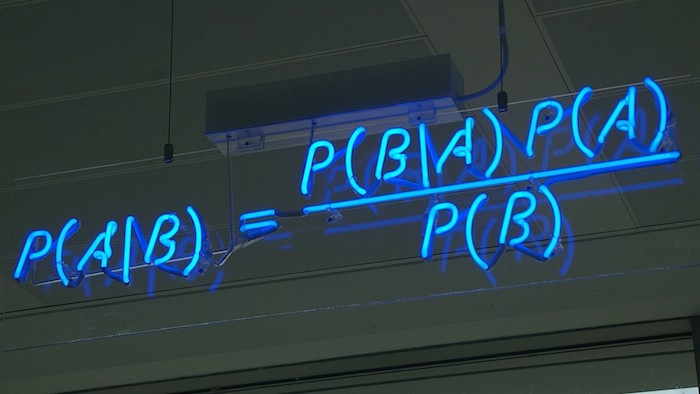Un’introduzione delicata ai linguaggi di programmazione probabilistica
La programmazione probabilistica sta diventando una delle aree di sviluppo più attive nello spazio di machine learning. Quali sono le principali lingue che dovremmo conoscere?

Il pensiero probabilistico è uno strumento incredibilmente prezioso per il processo decisionale. Dagli economisti ai giocatori di poker, le persone che possono pensare in termini di probabilità tendono a prendere decisioni migliori di fronte a situazioni incerte. I campi delle probabilità e della teoria dei giochi sono stati stabiliti per secoli e decenni ma non stanno vivendo un rinascimento con la rapida evoluzione dell’intelligenza artificiale (AI). Possiamo incorporare le probabilità come cittadini di prima classe di codice software? Benvenuti nel mondo dei linguaggi di programmazione probabilistica (PPL)
L’uso delle statistiche per superare l’incertezza è uno dei pilastri di un ampio segmento del mercato dell’apprendimento automatico. Il ragionamento probabilistico è stato a lungo considerato uno dei fondamenti degli algoritmi di inferenza ed è rappresentato da tutti i principali framework e piattaforme di machine learning. Recentemente, il ragionamento probabilistico ha visto l’adozione importante all’interno di giganti della tecnologia come Uber, Facebook o Microsoft, contribuendo a spingere l’agenda di ricerca e tecnologia nello spazio. In particolare, i PPL sono diventati una delle aree di sviluppo più attive nell’apprendimento automatico, scatenando il rilascio di alcune nuove ed entusiasmanti tecnologie.
Quali sono i linguaggi di programmazione probabilistica?
Concettualmente, i linguaggi di programmazione probabilistica (PPL) sono linguaggi specifici del dominio che descrivono i modelli probabilistici e la meccanica per eseguire l’inferenza in tali modelli. La magia di PPL si basa sulla combinazione delle capacità di inferenza dei metodi probabilistici con il potere rappresentativo dei linguaggi di programmazione.
In un programma PPL, le ipotesi sono codificate con distribuzioni precedenti sulle variabili del modello. Durante l’esecuzione, un programma PPL avvierà una procedura di inferenza per calcolare automaticamente le distribuzioni posteriori dei parametri del modello sulla base dei dati osservati. In altre parole, l’inferenza regola la distribuzione precedente usando i dati osservati per fornire una modalità più precisa. L’output di un programma PPL è una distribuzione di probabilità, che consente al programmatore di visualizzare e manipolare esplicitamente l’incertezza associata a un risultato.
Per illustrare la semplicità dei PPL, utilizziamo uno dei problemi più famosi della statistica moderna: un lancio di monete parziale. L’idea di questo problema è calcolare la propensione di una moneta. Supponiamo che xi = 1 se il risultato dell’i-esimo lancio della moneta è testa e xi = 0 se è coda. Il nostro contesto presuppone che i lanci individuali delle monete siano indipendenti e identicamente distribuiti (IID) e che ogni lancio segua una distribuzione di Bernoulli con il parametro θ: p (xi = 1 | θ) = θ e p (xi = 0 | θ) = 1 – θ . La variabile latente (cioè non osservata) θ è il bias della moneta. Il compito è inferire θ dati i risultati di lanci di monete precedentemente osservati, ovvero p (θ | x1, x2,…, XN).

Modellare un programma semplice come il lancio parziale di una moneta in un linguaggio di programmazione generico può risultare su centinaia di righe di codice. Tuttavia, PPL come Edward esprimono questo problema in alcuni semplici mi piace del codice:

Modello

theta = Uniform (0.0, 1.0)
x = Bernoulli (probs = theta, sample_shape = 10)
Dati 5 dati = np.array ([0, 1, 0, 0, 0, 0, 0, 0, 0, 1 ])
Inferenza
qtheta = Empirical (8 tf.Variable (tf.ones (1000) ∗ 0.5))
inferenza = ed.HMC ({theta: qtheta},
data = {x: data})
inference.run ()
Risultati 13 media , stddev = ed.get_session (). run ([qtheta.mean (), qtheta.stddev ()])
print (“Posterior mean:”, mean)
print (“Posterior stddev:”, stddev)
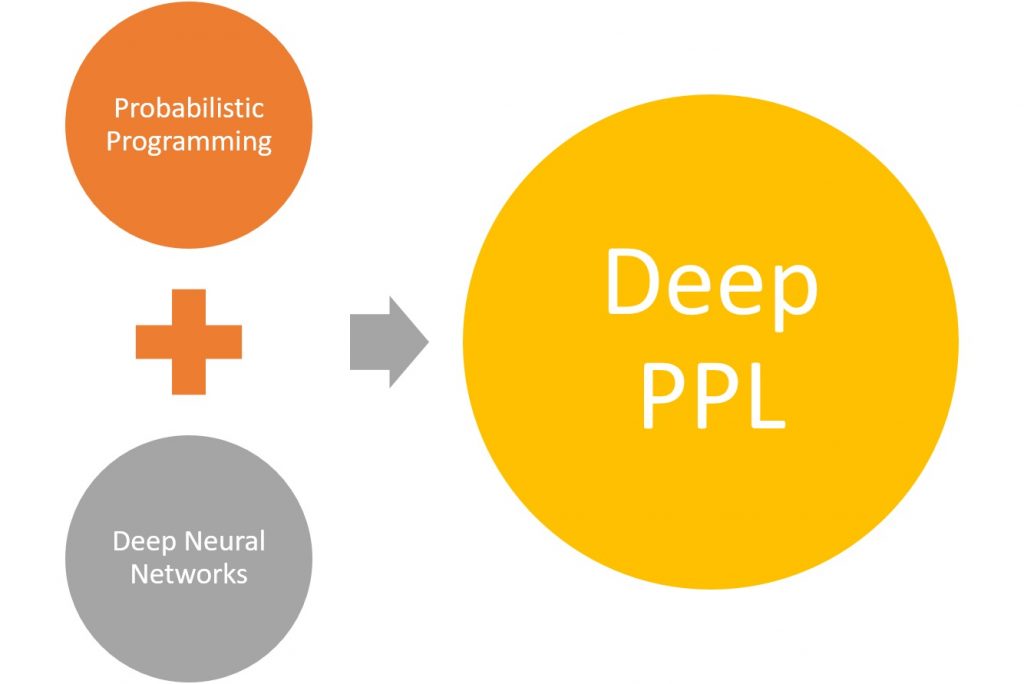
Il Santo Graal: Deep PPL
Per decenni, lo spazio dell’apprendimento automatico è stato diviso in due campi inconciliabili: statistiche e reti neurali. Un campo ha dato vita alla programmazione probabilistica mentre l’altro era dietro a movimenti di trasformazione come l’apprendimento profondo. Di recente, le due scuole di pensiero si sono unite per combinare l’apprendimento profondo e la modellistica bayesiana in singoli programmi. La massima espressione di questo sforzo sono i linguaggi di programmazione probabilistica profonda (Deep PPLs).

Concettualmente, i Deep PPL possono esprimere le reti neurali bayesiane con pesi e preconcetti probabilistici. In pratica, i Deep PPL si sono materializzati come nuovi linguaggi probabilistici e librerie che si integrano perfettamente con i più diffusi framework di deep learning.
3 PPL profondi che devi conoscere
Il campo dei linguaggi di programmazione probabilistica (PPL) è esploso con la ricerca e l’innovazione negli ultimi anni. Gran parte di queste innovazioni derivano dalla combinazione di PPL e metodi di apprendimento profondo per costruire reti neurali in grado di gestire efficacemente l’incertezza. Giganti della tecnologia come Google, Microsoft o Uber sono stati responsabili di spingere i confini dei Deep PPL in scenari su larga scala. Tali sforzi si sono tradotti in stack Deep PPL completamente nuovi che stanno diventando sempre più popolari all’interno della comunità dell’apprendimento automatico. Esploriamo alcuni dei più recenti progressi nello spazio Deep PPL.
Edward
Edward è un linguaggio di programmazione probabilistico (PPL) completo di Turing scritto in Python. Edward è stato originariamente sostenuto dal team di Google Brain ma ora ha un ampio elenco di collaboratori . Il documento di ricerca originale di Edward è stato pubblicato a marzo 2017 e da allora lo stack ha visto molte adozioni all’interno della comunità dell’apprendimento automatico. Edward fonde tre campi: statistica bayesiana e apprendimento automatico, apprendimento profondo e programmazione probabilistica. La biblioteca si integra perfettamente con i framework di deep learning come Keras e TensorFlow.
1 # Modello
2 theta = Uniform (0,0, 1,0)
3 x = Bernoulli (probs = theta, sample_shape = 10)
4 # Data
5 data = np.array ([0, 1, 0, 0, 0, 0, 0, 0, 0, 1])
6 # Inferenza
7 qtheta = Empirical (
8 tf.Variable (tf.ones (1000) ∗ 0.5))
9 inferference = ed.HMC ({theta: qtheta},
10 data = {x: data })
11 inference.run ()
12 # Risultati
13 media, stddev = ed.get_session (). Run (
14 [qtheta.mean (), qtheta.stddev ()])
15 print (“Media posteriore:”, media)
16 print (“Posterior stddev:”, stddev)
1 # Guida alle inferenze
2 qalpha = tf.Variable (1.0)
3 qbeta = tf.Variable (1.0)
4 qtheta = Beta (qalpha, qbeta)
5 # Inference
6 inferenza = ed.KLqp ({theta: qtheta}, {x: data})
7 inference.run ()
Pyro
Pyro è un linguaggio di programmazione probabilistico profondo (PPL) rilasciato da Uber AI Labs. Pyro si basa su PyTorch e si basa su quattro principi fondamentali:
Universale : Pyro è una PPL universale – può rappresentare qualsiasi distribuzione di probabilità calcolabile. Come? Partendo da un linguaggio universale con iterazione e ricorsione (codice Python arbitrario), quindi aggiungendo campionamento, osservazione e inferenza casuali.
Scalabile : Pyro si adatta a grandi set di dati con un piccolo overhead sopra il codice scritto a mano. Come? Sviluppando moderne tecniche di ottimizzazione della scatola nera, che utilizzano mini-lotti di dati, per approssimare l’inferenza.
Minimo : Pyro è agile e mantenibile. Come? Pyro è implementato con un piccolo nucleo di astrazioni potenti e compostabili. Ove possibile, il sollevamento di carichi pesanti è delegato a PyTorch e ad altre biblioteche.
Flessibile : Pyro punta all’automazione quando lo desideri e al controllo quando ne hai bisogno. Come? Pyro utilizza astrazioni di alto livello per esprimere modelli generativi e di inferenza, consentendo agli esperti di personalizzare facilmente l’inferenza.
Proprio come altri PPL, Pyro combina modelli di apprendimento profondo e inferenza statistica usando una sintassi semplice come illustrato nel seguente codice:
1 # Modello
2 def coin ():
3 theta = pyro.sample (“theta”, Uniform (
4 Variable (torch.Tensor ([0])),
5 Variable (torch.Tensor ([1])))
6 pyro .sample (“x”, Bernoulli (
7 theta ∗ Variable (torch.ones (10)))
8 # Data
9 data = {“x”: Variable (torch.Tensor (
10 [0, 1, 0, 0, 0 , 0, 0, 0, 0, 1]))}
11 # Inference
12 cond = pyro.condition (coin, data = data)
13 sampler = pyro.infer.Importance (cond,
14 num_samples = 1000)
15 post = pyro .infer.Marginal (sampler, sites = [“theta”])
16 # Risultato
17 samples = [post () [“theta”]. data [0] for _ in range (1000)]
18 print (“Media posteriore: “, np.mean (campioni))
19 print (“Posterior stddev:”, np.std (samples)) # Inference Guide
2 def guide ():
3 qalpha = pyro.param (“qalpha”, Variable (torch.Tensor ([1.0]), richiede_grad = True ))
4 qbeta = pyro.param (“qbeta”, variabile (torch.Tensor ([1.0]), richiede_grad = True))
5 pyro.sample (“theta”, Beta (qalpha, qbeta))
6 # Inference
7 svi = SVI (cond, guide, Adam ({}), loss = “ELBO”, num_particles = 7)
8 per step in range (1000):
9 svi.step ()
Infer.Net
Microsoft ha recentemente aperto Infer.Net di provenienza un framework che semplifica la programmazione probabilistica per gli sviluppatori .Net. Microsoft Research lavora su Infer.Net dal 2004 ma è stato solo di recente, con l’emergere del deep learning, che il framework è diventato molto popolare. Infer.Net offre alcuni forti differenziatori che lo rendono una scelta forte per gli sviluppatori che si avventurano nello spazio Deep PPL:
Rich modeling language ”Supporto per variabili univariate e multivariate, sia continue che discrete. I modelli possono essere costruiti da una vasta gamma di fattori tra cui operazioni aritmetiche, algebra lineare, vincoli di intervallo e positività, operatori booleani, Dirichlet-Discrete, gaussiano e molti altri.
Algoritmi a inferenza multipla ”Gli algoritmi integrati includono Propagazione delle aspettative, Propagazione del credo (un caso speciale di EP), Passaggio di messaggi variazionali e campionamento di Gibbs.
Progettato per inferenze su larga scala : Infer.NET compila i modelli in codice sorgente di inferenza che può essere eseguito indipendentemente senza sovraccarico. Può anche essere integrato direttamente nella tua applicazione.
Estensibile dall’utente : l’utente può aggiungere distribuzioni di probabilità, fattori, operazioni sui messaggi e algoritmi di inferenza. Infer.NET utilizza un’architettura plug-in che la rende aperta e adattabile.
Vediamo il nostro esempio di lancio di monete in Infer.Net
Variabile firstCoin = Variable.Bernoulli (0,5);
Variabile secondCoin = Variable.Bernoulli (0,5);
Variabile bothHeads = firstCoin & secondCoin;
InferenceEngine engine = new InferenceEngine ();
Console.WriteLine (“Probabilità entrambe le monete sono teste:” + engine.Infer (bothHead));
Il campo di Deep PPL sta diventando costantemente un importante blocco fondamentale dell’ecosistema di machine learning. Pyro, Edward e Infer.Net sono solo tre esempi recenti di Deep PPL ma non gli unici rilevanti. L’intersezione di framework di deep learning e PPL offre un’incredibile impronta di grandi dimensioni per l’innovazione e nuovi casi d’uso probabilmente spingeranno i confini dei Deep PPL nel prossimo futuro.