Che cos’è la riduzione della dimensionalità?
Più dimensioni portano a un overfittingMetodi comuni di riduzione della dimensionalità
La riduzione della dimensionalità è un processo utilizzato per ridurre la dimensionalità di un set di dati, prendendo molte caratteristiche e rappresentandole come meno caratteristiche. Ad esempio, la riduzione della dimensionalità potrebbe essere utilizzata per ridurre un set di dati di venti funzionalità fino a poche funzionalità. La riduzione della dimensionalità viene comunemente utilizzata nelle attività di apprendimento senza supervisione per creare automaticamente classi da molte funzionalità. Per capire meglio perché e come viene utilizzata la riduzione della dimensionalità , daremo uno sguardo ai problemi associati ai dati ad alta dimensione e ai metodi più diffusi per ridurre la dimensionalità.
Più dimensioni portano a un overfitting
La dimensionalità si riferisce al numero di caratteristiche / colonne all’interno di un set di dati.
Si presume spesso che nell’apprendimento automatico più funzionalità siano migliori, poiché crea un modello più accurato. Tuttavia, più funzionalità non si traducono necessariamente in un modello migliore.
Le caratteristiche di un set di dati possono variare ampiamente in termini di utilità per il modello, con molte caratteristiche di poca importanza. Inoltre, più funzionalità contiene il set di dati, più campioni sono necessari per garantire che le diverse combinazioni di funzionalità siano ben rappresentate all’interno dei dati. Pertanto, il numero di campioni aumenta in proporzione al numero di funzioni. Più campioni e più funzionalità significano che il modello deve essere più complesso e, man mano che i modelli diventano più complessi, diventano più sensibili all’overfitting. Il modello apprende troppo bene i modelli nei dati di addestramento e non riesce a generalizzare a dati fuori campione.
La riduzione della dimensionalità di un set di dati ha diversi vantaggi. Come accennato, i modelli più semplici sono meno inclini all’overfitting, poiché il modello deve fare meno ipotesi su come le funzionalità sono correlate l’una all’altra. Inoltre, un numero inferiore di dimensioni significa una minore potenza di calcolo necessaria per addestrare gli algoritmi. Allo stesso modo, è necessario meno spazio di archiviazione per un set di dati con dimensionalità inferiore. La riduzione della dimensionalità di un set di dati può anche consentire di utilizzare algoritmi non adatti a set di dati con molte funzionalità.
Metodi comuni di riduzione della dimensionalità
La riduzione della dimensionalità può avvenire tramite la selezione delle caratteristiche o l’ingegneria delle caratteristiche. La selezione delle funzionalità è il punto in cui l’ingegnere identifica le funzionalità più rilevanti del set di dati, mentre l’ ingegneria delle funzionalità è il processo di creazione di nuove funzionalità combinando o trasformando altre funzionalità.
La selezione e la progettazione delle funzionalità possono essere eseguite a livello di programmazione o manualmente. Quando si selezionano e si ingegnerizzano manualmente le caratteristiche, è tipico visualizzare i dati per scoprire le correlazioni tra le caratteristiche e le classi. Effettuare la riduzione della dimensionalità in questo modo può richiedere molto tempo e quindi alcuni dei modi più comuni per ridurre la dimensionalità comportano l’uso di algoritmi disponibili in librerie come Scikit-learn for Python. Questi algoritmi comuni di riduzione della dimensionalità includono: analisi dei componenti principali (PCA), decomposizione dei valori singolari (SVD) e analisi discriminante lineare (LDA).
Gli algoritmi utilizzati nella riduzione della dimensionalità per attività di apprendimento non supervisionato sono tipicamente PCA e SVD, mentre quelli sfruttati per la riduzione della dimensionalità dell’apprendimento supervisionato sono tipicamente LDA e PCA. Nel caso di modelli di apprendimento supervisionato, le nuove funzionalità generate vengono semplicemente inserite nel classificatore di apprendimento automatico. Si noti che gli usi qui descritti sono solo casi d’uso generali e non le uniche condizioni in cui queste tecniche possono essere utilizzate. Gli algoritmi di riduzione della dimensionalità descritti sopra sono semplicemente metodi statistici e vengono utilizzati al di fuori dei modelli di apprendimento automatico.
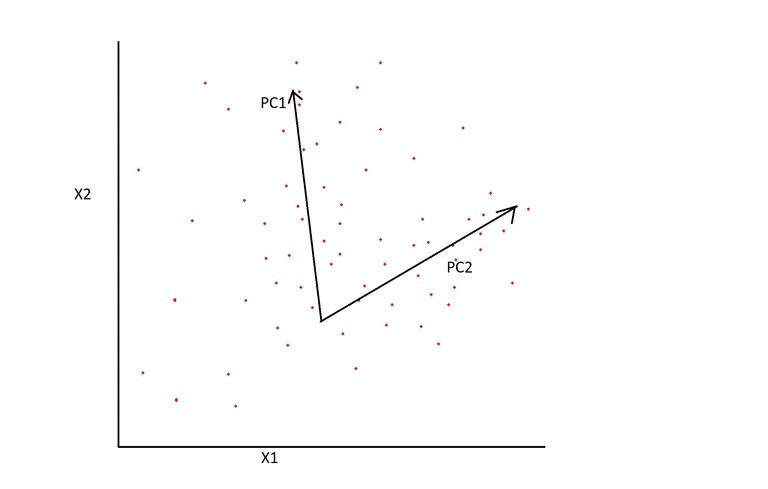
Analisi del componente principale
matrice con i componenti principali identificati
Principal Component Analysis (PCA) è un metodo statistico che analizza le caratteristiche / caratteristiche di un set di dati e riassume le caratteristiche che sono le più influenti. Le caratteristiche del set di dati sono combinate insieme in rappresentazioni che mantengono la maggior parte delle caratteristiche dei dati ma sono distribuite su meno dimensioni. Puoi pensare a questo come a “schiacciare” i dati da una rappresentazione di dimensione superiore a una con poche dimensioni.
Come esempio di una situazione in cui la PCA potrebbe essere utile, pensa ai vari modi in cui si potrebbe descrivere il vino. Sebbene sia possibile descrivere il vino utilizzando molte caratteristiche altamente specifiche come livelli di CO2, livelli di aerazione, ecc., Tali caratteristiche specifiche possono essere relativamente inutili quando si cerca di identificare un tipo specifico di vino. Invece, sarebbe più prudente identificare il tipo in base a caratteristiche più generali come gusto, colore ed età. La PCA può essere utilizzata per combinare funzionalità più specifiche e creare funzionalità più generali, utili e con meno probabilità di causare overfitting.
La PCA viene eseguita determinando come le caratteristiche di input variano dalla media l’una rispetto all’altra, determinando se esistono relazioni tra le caratteristiche. Per fare ciò viene creata una matrice covariante, stabilendo una matrice composta dalle covarianze rispetto alle possibili coppie delle caratteristiche del dataset. Viene utilizzato per determinare le correlazioni tra le variabili, con una covarianza negativa che indica una correlazione inversa e una correlazione positiva che indica una correlazione positiva.
I componenti principali (più influenti) del set di dati vengono creati creando combinazioni lineari delle variabili iniziali, che viene eseguita con l’assistenza di concetti di algebra lineare chiamati autovalori e autovettori . Le combinazioni vengono create in modo che i componenti principali non siano correlati tra loro. La maggior parte delle informazioni contenute nelle variabili iniziali è compressa nei primi pochi componenti principali, il che significa che sono state create nuove caratteristiche (le componenti principali) che contengono le informazioni dal dataset originale in uno spazio dimensionale più piccolo.
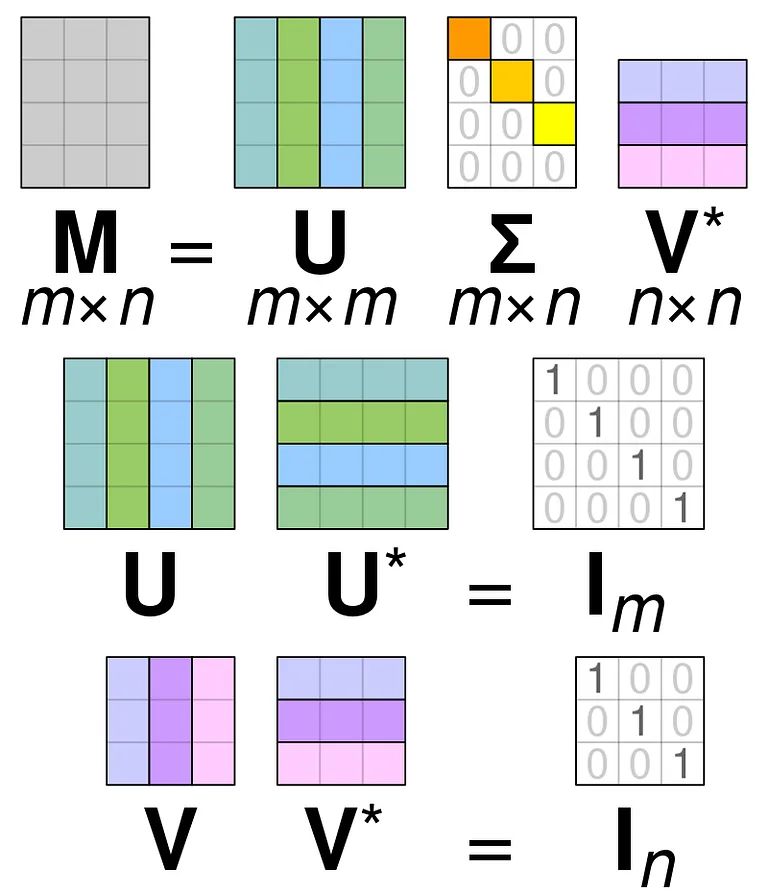
Scomposizione di un valore singolo
Singular Value Decomposition (SVD) viene utilizzato per semplificare i valori all’interno di una matrice , riducendo la matrice fino alle sue parti costituenti e semplificando i calcoli con quella matrice. SVD può essere utilizzato sia per matrici di valori reali che complesse, ma ai fini di questa spiegazione esaminerà come scomporre una matrice di valori reali.
Supponiamo di avere una matrice composta da dati di valore reale e il nostro obiettivo è ridurre il numero di colonne / caratteristiche all’interno della matrice, in modo simile all’obiettivo della PCA. Come PCA, SVD comprimerà la dimensionalità della matrice preservando il più possibile la variabilità della matrice. Se vogliamo operare sulla matrice A, possiamo rappresentare la matrice A come altre tre matrici chiamate U, D e V. La matrice A è composta dagli elementi x * y originali mentre la matrice U è composta dagli elementi X * X (è una matrice ortogonale). La matrice V è una diversa matrice ortogonale contenente elementi y * y. La matrice D contiene gli elementi x * y ed è una matrice diagonale.
Per scomporre i valori per la matrice A, è necessario convertire i valori della matrice singolare originale nei valori diagonali trovati all’interno di una nuova matrice. Quando si lavora con matrici ortogonali, le loro proprietà non cambiano se vengono moltiplicate per altri numeri. Pertanto, possiamo approssimare la matrice A sfruttando questa proprietà. Quando moltiplichiamo le matrici ortogonali insieme a una trasposizione di Matrix V, il risultato è una matrice equivalente alla nostra originale A.
Quando la matrice a viene scomposta nelle matrici U, D e V, contengono i dati trovati all’interno della matrice A. Tuttavia, le colonne più a sinistra delle matrici conterranno la maggior parte dei dati. Possiamo prendere solo queste prime poche colonne e avere una rappresentazione della matrice A che ha molte meno dimensioni e la maggior parte dei dati all’interno di A.
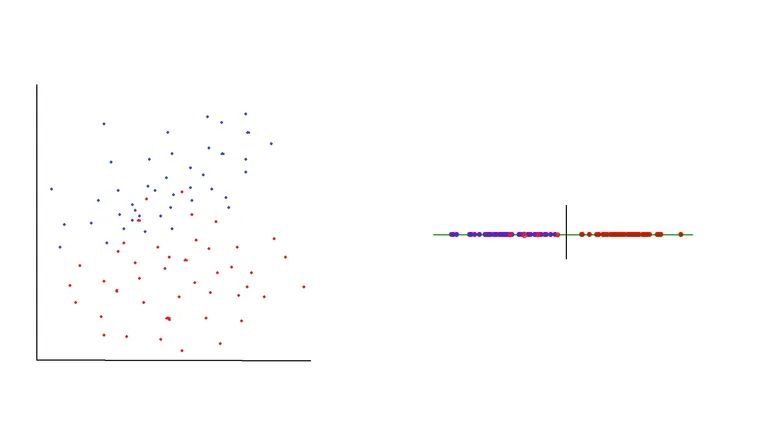
Analisi discriminante lineare
A sinistra: matrice prima di LDA, a destra: asse dopo LDA, ora separabile
Linear Discriminant Analysis (LDA) è un processo che prende i dati da un grafico multidimensionale e li riproietta su un grafico lineare . Puoi immaginarlo pensando a un grafico bidimensionale pieno di punti dati appartenenti a due classi diverse. Supponiamo che i punti siano sparsi in modo che non sia possibile tracciare una linea che separerà nettamente le due diverse classi. Per gestire questa situazione, i punti trovati nel grafico 2D possono essere ridotti a un grafico 1D (una linea). Questa linea avrà tutti i punti dati distribuiti su di essa e si spera possa essere divisa in due sezioni che rappresentano la migliore separazione possibile dei dati.
Nello svolgimento dell’ADL ci sono due obiettivi primari. Il primo obiettivo è ridurre al minimo la varianza per le classi, mentre il secondo obiettivo è massimizzare la distanza tra le medie delle due classi. Questi obiettivi vengono raggiunti creando un nuovo asse che esisterà nel grafico 2D. L’asse appena creato agisce per separare le due classi in base agli obiettivi precedentemente descritti. Dopo che l’asse è stato creato, i punti trovati nel grafico 2D vengono posizionati lungo l’asse.
Sono necessari tre passaggi per spostare i punti originali in una nuova posizione lungo il nuovo asse. Nella prima fase, la distanza tra le medie delle singole classi (la varianza tra le classi) viene utilizzata per calcolare la separabilità delle classi. Nella seconda fase viene calcolata la varianza all’interno delle diverse classi, effettuata determinando la distanza tra il campione e la media per la classe in questione. Nella fase finale, viene creato lo spazio di dimensione inferiore che massimizza la varianza tra le classi.
La tecnica LDA raggiunge i migliori risultati quando i mezzi per le classi target sono molto distanti l’uno dall’altro. LDA non può separare efficacemente le classi con un asse lineare se le medie per le distribuzioni si sovrappongono.