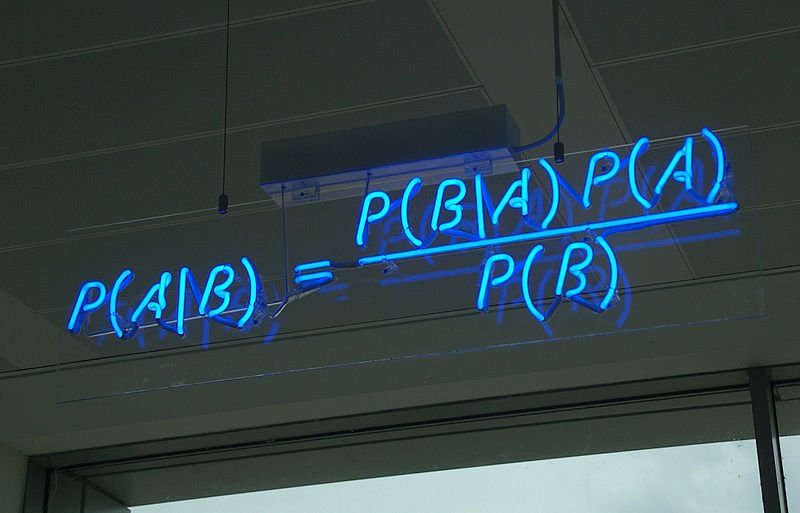di Daniel Nelson
Se hai imparato a conoscere la scienza dei dati o l’apprendimento automatico , ci sono buone probabilità di aver già sentito il termine “Teorema di Bayes” o un “classificatore di Bayes”. Questi concetti possono essere un po ‘confusi, specialmente se non sei abituato a pensare alla probabilità da una prospettiva statistica tradizionale e frequentista. Questo articolo tenterà di spiegare i principi alla base del teorema di Bayes e come viene utilizzato nell’apprendimento automatico.
Teorema della definizione di Bayes
Il teorema di Bayes è un metodo per calcolare la probabilità condizionale . Il metodo tradizionale di calcolo della probabilità condizionale (la probabilità che si verifichi un evento dato il verificarsi di un evento diverso) consiste nell’utilizzare la formula della probabilità condizionale, calcolando la probabilità congiunta dell’evento uno e dell’evento due che si verificano contemporaneamente, quindi dividendola dalla probabilità che si verifichi l’evento due. Tuttavia, la probabilità condizionale può anche essere calcolata in modo leggermente diverso usando il Teorema di Bayes.
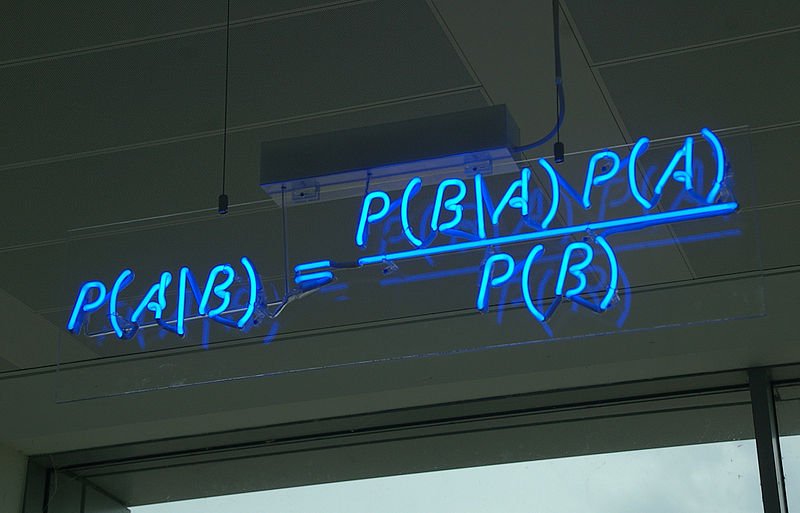
Quando si calcola la probabilità condizionale con il teorema di Bayes, utilizzare i seguenti passi:
Determina la probabilità che la condizione B sia vera, assumendo che la condizione A sia vera.
Determina la probabilità che l’evento A sia vero.
Moltiplica le due probabilità insieme.
Dividi per la probabilità che si verifichi l’evento B.
Ciò significa che la formula del teorema di Bayes potrebbe essere espressa in questo modo:
P (A | B) = P (B | A) * P (A) / P (B)
Il calcolo della probabilità condizionale in questo modo è particolarmente utile quando la probabilità condizionale inversa può essere facilmente calcolata o quando il calcolo della probabilità congiunta sarebbe troppo impegnativo.
Un esempio pratico
Questo potrebbe essere più facile da interpretare se passiamo un po ‘di tempo a guardare un esempio di come applicare il ragionamento bayesiano e il teorema di Bayes. Supponiamo che tu stia giocando a un semplice gioco in cui più partecipanti ti raccontano una storia e devi determinare quale dei partecipanti ti sta mentendo. Compiliamo l’equazione per il teorema di Bayes con le variabili in questo ipotetico scenario.
Stiamo cercando di prevedere se ogni individuo nel gioco sta mentendo o dicendo la verità, quindi se ci sono tre giocatori a parte te, le variabili categoriali possono essere espresse come A1, A2 e A3. L’evidenza per le loro bugie / verità è il loro comportamento. Come quando giochi a poker, dovresti cercare alcuni “racconti” che una persona sta mentendo e usarli come frammenti di informazioni per informare la tua ipotesi. O se ti fosse permesso di metterle in discussione, ci sarebbero prove che la loro storia non si sommi. Possiamo rappresentare la prova che una persona sta mentendo come B.
Per essere chiari, miriamo a prevedere la probabilità (A sta mentendo / dicendo la verità | dati l’evidenza del loro comportamento). Per fare ciò vorremmo capire la probabilità di B dato A, o la probabilità che il loro comportamento si verifichi dato che la persona ha veramente mentito o detto la verità. Stai cercando di determinare in quali condizioni il comportamento che vedi avrebbe più senso. Se ci sono tre comportamenti a cui stai assistendo, faresti il calcolo per ogni comportamento. Ad esempio, P (B1, B2, B3 * A). Lo faresti quindi per ogni ricorrenza di A / per ogni persona nel gioco a parte te stesso. Questa è questa parte dell’equazione sopra:
P (B1, B2, B3, | A) * P | A
Infine, lo dividiamo solo per la probabilità di B.
Se avessimo ricevuto prove circa le reali probabilità in questa equazione, ricreammo il nostro modello di probabilità, tenendo conto delle nuove prove. Questo si chiama aggiornamento dei tuoi priori, mentre aggiorni le tue ipotesi sulla probabilità precedente che si verifichino gli eventi osservati.
Applicazioni di apprendimento automatico
L’uso più comune del teorema di Bayes quando si tratta di apprendimento automatico è nella forma dell’algoritmo Naive Bayes.
Naive Bayes viene utilizzato per la classificazione di set di dati binari e multi-classe, Naive Bayes prende il nome perché i valori assegnati alle prove / attributi dei testimoni – Bs in P (B1, B2, B3 * A) – sono considerati indipendenti l’uno dall’altro. Si presume che questi attributi non si influenzino a vicenda al fine di semplificare il modello e rendere possibili i calcoli, invece di tentare il complesso compito di calcolare le relazioni tra ciascuno degli attributi. Nonostante questo modello semplificato, Naive Bayes tende a funzionare abbastanza bene come algoritmo di classificazione, anche quando questa ipotesi probabilmente non è vera (che è il più delle volte).
Esistono anche varianti comunemente usate del classificatore Naive Bayes, come Multinomial Naive Bayes, Bernoulli Naive Bayes e Gaussian Naive Bayes.
Gli algoritmi multinomiali Naive Bayes vengono spesso utilizzati per classificare i documenti, in quanto è efficace nell’interpretazione della frequenza delle parole all’interno di un documento.
Bernoulli Naive Bayes funziona in modo simile a Naive Bayes multinomiale, ma le previsioni rese dall’algoritmo sono booleane. Ciò significa che quando si prevede una classe i valori saranno binari, no o sì. Nel dominio della classificazione del testo, un algoritmo di Bernoulli Naive Bayes assegnerebbe ai parametri un sì o no in base alla presenza o meno di una parola nel documento di testo.
Se il valore dei predittori / funzionalità non è discreto ma è invece continuo, è possibile utilizzare Gaussian Naive Bayes . Si presume che i valori delle caratteristiche continue siano stati campionati da una distribuzione gaussiana.