MODELLO EPIDEMIOLOGICO GUIDATO DA ML PER PREVEDERE LA PROGRESSIONE DI COVID-19 MEDIANTE LA QUANTIFICAZIONE DEGLI INTERVENTI
L’Organizzazione Mondiale della Sanità ha dichiarato COVID-19 come una pandemia l’11 marzo ° , 2020. L’esplosione dei casi segnalati a livello mondiale da allora è fortemente cresciuta, impattando la vita giorno per giorno di entrambe le organizzazioni e individui in tutto il mondo. È ora indispensabile capire quanto potrebbe durare la pandemia e trovare modi efficaci per appiattire la progressione dei casi COVID-19.
La letteratura di ricerca copre vari modelli statistici (come la distribuzione gamma , distribuzioni binomiali negative ) e modelli epidemiologici (come SIR, SEIR) che vengono utilizzati per fare previsioni sul numero di persone infette da malattie contagiose come Ebola, SARS, MERS. Tuttavia, la ricerca sulla velocità di trasmissione, il periodo di incubazione e altri parametri che vanno alla modellizzazione matematica della diffusione di COVID-19 è ancora in una fase nascente con la maggior parte di essa ancora da rivedere.
Pertanto, i modelli epidemiologici autonomi potrebbero non essere sufficienti per prevedere la diffusione di Covid-19. Inoltre, questi parametri possono variare in base alla regione e alle misure di intervento intraprese da vari governi come l’allontanamento sociale, la chiusura delle scuole, i blocchi completi e così via. In questo articolo, presentiamo una soluzione predittiva di ensemble che combina un modello epidemiologico e varie tecniche di Machine Learning (ML) per prevedere l’impatto del COVID-19. La soluzione incorpora anche le misure di intervento adottate da vari governi per frenare l’impatto.
introduzione
I metodi usati frequentemente per prevedere la crescita di qualsiasi malattia infettiva includono l’uso di modelli epidemiologici . Mostriamo due di questi modelli epidemiologici comunemente usati nella figura seguente:

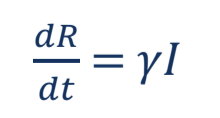
Modello SIR – Come mostrato in Fig. 1, ‘S’ indica la proporzione di una popolazione che è suscettibile, ‘I’ è il numero di persone infette e ‘R’ rappresenta il numero di pazienti recuperati. N è definita come la somma di ‘S’, ‘I’ e ‘R’, che è costante e considerata come la popolazione totale della regione di previsione. Il modello SIR può essere rappresentato dalle equazioni seguenti:
Modello SEIR – “S” indica la percentuale di popolazione suscettibile, “I” è il numero di persone infette, “R” è la percentuale di pazienti guariti e “E” indica le persone che sono state esposte alla malattia ma non lo sono infettiva. Il modello SEIR può essere rappresentato dalle equazioni riportate di seguito:
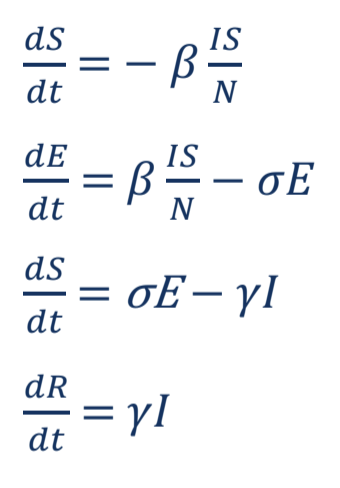
Nelle equazioni per entrambi i modelli, il tasso infettivo è indicato con β ed è rappresentativo della probabilità di trasmissione della malattia tra persone sensibili e infettive. Allo stesso modo, il tasso di incubazione della malattia è rappresentato da σ e il tasso di recupero del paziente è rappresentato da γ.


Figura 1 – Una rappresentazione illustrativa della tradizionale a. SIR e b. Modelli SEIR
Soluzione di previsione delle malattie Covid-19
In questa sezione, approfondiamo la soluzione di previsione di Genpact. La soluzione prevede tre passaggi principali:
Creazione del modello SIDR: viene creato un solutore per l’insieme di equazioni differenziali che rappresentano il modello SIDR (Susceptible-Infected-Dead-Recovered) utilizzando TensorFlow (libreria di probabilità TensorFlow) e parametri iniziali per il modello epidemiologico.
Quantificare gli interventi: l’impatto di interventi come blocchi e regolamenti di allontanamento sociale da parte delle autorità governative è incorporato dinamicamente nel modello.
Riduzione al minimo degli errori con ML: un modello di apprendimento automatico multi-obiettivo viene creato utilizzando l’ottimizzatore di Adam di TensorFlow per identificare i casi, i decessi e le curve di recupero che si adattano meglio alle curve effettive riportate finora.
Leggi anche COVID-19: Un contributo degli scienziati dei dati nel mantenimento della salute fisica e del benessere spiegato
Modello SIDR
Il modello SIR modificato (ovvero SIDR) consente di modellare la progressione dei casi COVID-19 utilizzando i dati aggiornati quotidianamente di casi confermati, decessi e recuperi, come riportato sul sito Web della Johns Hopkins University (JHU) . Inoltre, i parametri per ciascuno di questi attributi sono stati calcolati utilizzando un modello di Machine Learning (ML). Sulla base dei dati di JHU, i seguenti attributi sono stati inclusi nella metodologia di previsione:
Numero di casi confermati COVID-19 in ciascuno stato negli Stati Uniti
Numero di decessi per COVID-19 in ciascuno stato negli Stati Uniti
Numero di pazienti che si sono ripresi dopo aver contratto COVID-19 in ciascuno stato
Nel modello proposto, abbiamo scelto di non utilizzare SEIR come modello epidemiologico perché i dati e la ricerca sulla componente Esposta (numero di individui esposti ma non attualmente infettivi) sono relativamente sconosciuti.
La soluzione utilizza invece “il modello SIR con una variabile aggiunta D” – con D che rappresenta il numero di decessi per COVID-19. Tenendo conto dei decessi, il sistema di equazioni differenziali ordinarie (ODE) utilizzato nella soluzione è riportato di seguito:
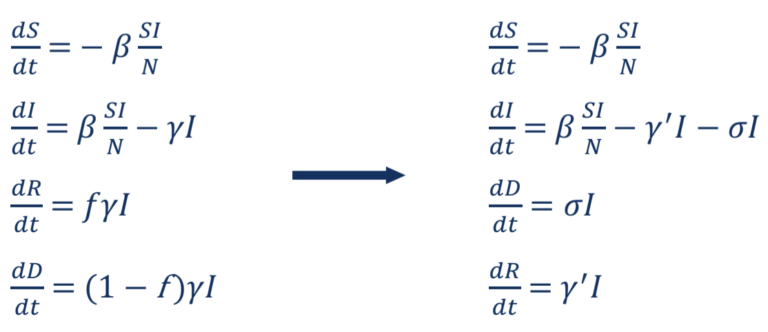
La f nel sistema di equazioni differenziali (a sinistra) indica la percentuale di persone infette che moriranno a causa dell’infezione. Si può dimostrare matematicamente che il sistema di ODE a sinistra è equivalente al sistema di ODE a destra, che può quindi essere usato per modellare morti e recuperi in modo indipendente.
Figura 3 – Flusso di lavoro del modello COVID-19 ML utilizzando il modello epidemiologico SIDR
La metodologia prevede quindi la minimizzazione dell’errore simultaneo per casi confermati, decessi e recuperi tra le serie temporali proiettate utilizzando il modello SIDR e le serie temporali dai dati effettivi. Pertanto, i parametri – tasso di infezione, tasso di mortalità e tasso di recupero vengono addestrati utilizzando il modello di apprendimento automatico.
Modellare l’impatto del blocco e degli interventi.
Una volta che la progressione effettiva è stata modellata utilizzando i metodi SIDR, gli errori nella frequenza infetta prevista, nella percentuale di mortalità e nella percentuale di recupero sono ridotti al minimo utilizzando una funzione di minimizzazione multi-obiettivo. Gli interventi richiesti dai governi di tutto il mondo (come blocchi, distanziamento sociale, chiusura di scuole e bar, ecc.) Incidono sul movimento delle persone in una regione. Poiché la riduzione della mobilità in una regione è direttamente correlata agli interventi , il coronavirus non si diffonde allo stesso ritmo di prima che tali interventi fossero imposti. Pertanto, il modello è stato progettato per utilizzare i dati sulla mobilità della posizione per prevedere la progressione di COVID-19 per tenere conto dinamicamente degli interventi del governo.
Leggi anche COVID-19 costringe Samsung e LG a mettere fabbriche bloccate
Il modello presuppone che, sotto blocco, il tasso di infezione diminuisca esponenzialmente con il passare del tempo. Due date separate che definiscono la data di inizio dell’intervento e la data di inizio del blocco sono state calcolate dai dati di mobilità (variazione% dei movimenti nella regione). Il punto di soglia per la data di intervento è stato preso quando la mobilità diminuisce di almeno il 30%.
La seguente equazione è stata utilizzata per incorporare nel modello gli effetti dei blocchi e del distanziamento sociale:
Dove 1 e 2 sono parametri di decadimento formati dal modello T i e t l sono date in cui l’intervento e inizio di blocco
Pertanto, il termine β nel modello SIDR non è una costante, ma piuttosto una variabile dipendente dal tempo modellata da α 1 e α 2 . Il modello può anche tornare indietro attraverso i dati del mondo reale per prevedere scenari di infezione, mortalità e tassi di guarigione, se le misure di blocco in uno stato fossero iniziate 2-3 settimane prima dell’attuazione effettiva. Inoltre, il modello può anche prevedere situazioni come casi in cui i blocchi vengono revocati dopo 2-3 settimane, in futuro.
La soluzione prevede diverse variabili tra cui: identificazione delle curve di picco e di recupero, casi confermati, decessi e tassi di recupero, in ciascuna regione. La soluzione è stata sviluppata per ciascuno dei 50 stati negli Stati Uniti ed è espandibile in tutte le regioni del mondo.
risultati
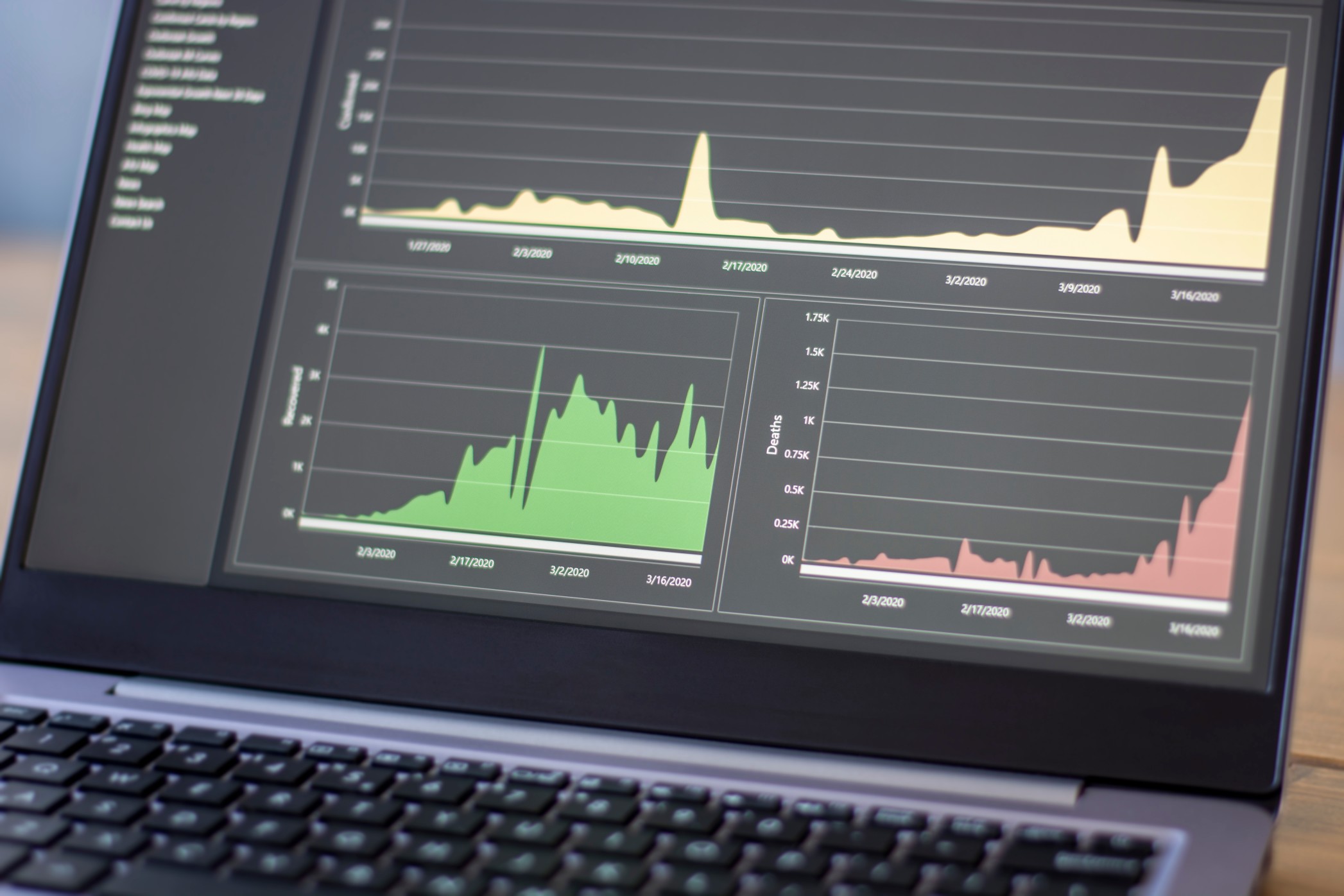
In questa sezione, presentiamo la diffusione della malattia COVID-19 in uno degli stati (Connecticut) negli Stati Uniti. Il modello è stato addestrato su dati storici (12 ° marzo – 25 ° aprile 2020) di casi confermati, morti e recuperi, per prevedere la progressione della malattia nei prossimi 45 giorni (fino al 9 ° giugno 2020). La misura dell’accuratezza utilizzata per l’addestramento del modello era l’errore ponderato medio assoluto ponderato (MAPE) su casi confermati, decessi e recuperi, agendo così come una funzione di minimizzazione multi-obiettivo. Per il periodo invisibile, le previsioni future per i casi confermati hanno comportato una settimana fuori e due settimane fuori MAPE, rispettivamente del 12% e del 15%.
Fig. 4 mostra le curve per giornaliero effettivo COVID -19 casi contro i casi quotidiani previsti fino a 25 ° aprile 2020 per capire come i casi previsti siano allineati con casi reali. Fig. 5, rappresenta la morte giornaliero effettivo contro le morti previste sino 25 th Aprile 2020. Fig. 6, Rappresenta i recuperi giornaliero effettivo rispetto dei recuperi previsti sino 25 th Aprile 2020. Fig. 7, spettacoli proiezione degli quotidiano casi confermati di rappresentare la progressione della malattia in Connecticut. La curva mostra che la malattia raggiungerà il picco da metà aprile a metà maggio e gradualmente diminuirà entro la fine di giugno. Mostra anche i decessi e i recuperi, che dovrebbero aumentare verso la fine di giugno a causa del periodo di incubazione del virus e del tempo trascorso negli ospedali dopo aver contratto un’infezione.
Leggi anche il rilascio di COVID-19 Datahub e un invito all’azione con AI
Figura – 4
Figura – 5
Figura – 6
Figura – 7
Potenziali aree di applicazione
Il modello di previsione COVID-19 è estremamente utile in casi d’uso come:
Previsione del letto e del ventilatore ICU – A causa del rapido aumento del numero di casi confermati di COVID-19 e della maggior parte dei governi di tutto il mondo che cercano di “appiattire la curva del tasso di infezione”, la disponibilità di letti di terapia intensiva è diventata fondamentale. La previsione del numero di letti e ventilatori disponibili in terapia intensiva darà agli ospedali un’idea di come possono trattare i pazienti in arrivo ed evitare alti tassi di mortalità e ridurre la durata dei pazienti critici in ospedale. La soluzione può aiutare a identificare il possibile numero di nuovi casi di infezione in una regione e potrebbe sorgere il numero previsto di ICU / requisiti del ventilatore.
Valutazione del rischio dei dipendenti : il modello può anche essere inserito con altre risorse disponibili al pubblico per la diffusione del virus e per i dati relativi ai siti e alle sedi di un’azienda. Ciò aiuterà l’azienda a prevedere il rischio che un dipendente venga esposto al coronavirus. Inoltre, il modello può essere migliorato in modo dinamico aggiungendo informazioni sui dipendenti come dati demografici e altri dati sullo stile di vita esterno per prevedere l’impatto sulle vendite, sulle capacità operative dell’azienda.
Nuova prospettiva aziendale normale – La pandemia di COVID-19 sta modificando drasticamente la domanda di prodotti da parte dei clienti. La soluzione può essere applicata per prevedere la domanda dei clienti per prevedere il nuovo comportamento dei consumatori o come cambieranno i volumi di vendita quando l’attività economica riprenderà nel periodo di recupero dopo la pandemia. La soluzione può anche aiutare le aziende a valutare le migliori pratiche per i nuovi modi normali di funzionare nel mondo post COVID-19, sviluppando un modello di rilevamento della domanda collegato ad indicatori esterni.