Quantificare e prevedere il successo nel mondo dello spettacolo

Quantificare e prevedere il successo nel mondo dello spettacolo
di Oliver E. Williams ,Lucas Lacasa eVito Latora
Nature Communications 10 , Articolo numero: 2256 ( 2019 )

Astratto
In alcuni tentativi artistici – come recitare in film e in TV, dove i tassi di disoccupazione oscillano intorno al 90% – la produttività sostenibile (semplicemente guadagnandosi da vivere) è probabilmente un proxy migliore per quantificare il successo piuttosto che un impatto elevato. Basandosi su un database mondiale, qui studiamo i profili temporali dell’attività di attori e attrici. Dimostriamo che la dinamica dell’assegnazione del lavoro è ben descritta da un meccanismo “ricco di ricchezze” e scopriamo che, mentre la percentuale di una carriera spesa attiva è imprevedibile, tale attività è raggruppata. Inoltre, la produttività tende ad essere più alta all’inizio della carriera e ci sono segnali che precedono l’anno più produttivo. Di conseguenza, proponiamo un metodo di apprendimento automatico che prevede con una precisione dell’85% se questo “annus mirabilis” è passato, o se i giorni migliori devono ancora venire.

introduzione
“È festa o carestia nel mondo dello spettacolo.” – Joan Rivers. Un sentimento probabilmente suscitato da molti sarebbe stelle dello schermo d’argento. Ma per coloro che festeggiano i premi, almeno pensavano di essere, vale la pena rischiare. La cosiddetta scienza del successo ha recentemente scoperto molte caratteristiche delle carriere di accademici 1 , artisti 2 e tutti i tipi di altre persone la cui produzione può essere valutata efficacemente nel corso della loro vita lavorativa 3 , 4 , 5 . Ad esempio, nel mondo della ricerca scientifica ha rivelato l’imprevedibilità dell’ubicazione di un lavoro accademico di maggior impatto 1 , dimostrando che anche premi così prestigiosi come i premi Nobel, che di solito si verificano successivamente in una carriera 6, sono sostenuti da documenti di ricerca che si trovano casualmente e in modo uniforme in tutto l’elenco ordinato di documenti nella carriera del premiato. D’altra parte, l’anatomia dei finanziamenti e delle collaborazioni nelle università ha rivelato “club ricchi” di istituzioni leader e ha suggerito che tali modelli di collaborazione contribuiscono notevolmente al successo di queste istituzioni, misurato in termini di eccessiva attrazione delle risorse disponibili e di ampiezza e profondità dei loro prodotti di ricerca 7 . Gli studi sull’innovazione nell’industria in diversi paesi hanno rilevato che il successo commerciale degli impianti di produzione è molto più strettamente correlato ai legami intragruppo rispetto ai legami esterni 8 . Sorprendentemente, queste caratteristiche possono essere comuni in più aree; l’effetto Matteo 9, 10 , o il fenomeno ricco di ricchezze, e la presenza recentemente scoperta di “hot streaks” 11 , non sono limitate a casi isolati. Per quanto riguarda il successo, è stato fatto molto lavoro nel valutare l’impatto 1 , 12 , la distribuzione di opere standout o landmark 13 , 14 , se queste sono legate all’età dell’individuo in questione 15 , 16 , come l’impatto può essere valutato a lungo termine 17 , e anche la previsione di futuri successi 18 , 19 . In effetti, le fortune di entrambi i film e gli attori e le attrici che li hanno fatti sono stati studiati in alcuni modi specifici17 , 20 , 21 , 22 . Questi studi non affrontano comunque la domanda che interessa quelli che non sono già sui gradini più alti della scala del successo: come si può evitare la carestia e costruire una carriera sostenibile nella recitazione?

Lo scopo di questo lavoro è di utilizzare un approccio basato sui dati al fine di definire, quantificare e persino prevedere il successo di attori e attrici in termini di capacità di mantenere un flusso costante di posti di lavoro. Basandosi sull’International Movie Database (IMDb), un database online di informazioni relative a film, programmi televisivi e video domestici, www.imdb.com , studiamo le carriere di milioni di attori di diversi paesi in tutto il mondo, dalla nascita del film a 1888 fino ai giorni nostri. Ogni carriera è vista come una sequenza di profili: le serie temporali annuali di lavori di recitazione in film o serie TV durante l’intera vita lavorativa dell’attore o attrice (questo è simile nello spirito all’approccio usato in 23per esplorare la produttività scientifica). Si noti che tutti i lavori di recitazione sono considerati, indipendentemente dal salario, dal ruolo, dallo schermo o dall’impatto del lavoro. L’analisi statistica di un numero così elevato di sequenze di profili ci consente di ricavare alcune proprietà generali dei modelli di attività degli attori. In particolare, esaminiamo diverse quantità di interesse come la durata della carriera, la produttività (definita come il numero di lavori di credito in un anno o nell’intera carriera di un attore) e la posizione dell’annus mirabilis, definita come l’anno con il più grande numero di lavori accreditati. Esploriamo anche la possibile comparsa di disuguaglianza di genere in queste proprietà.

Il primo messaggio che emerge dalla nostra analisi quantitativa è che le meraviglie di un solo colpo, cioè gli attori la cui carriera dura solo un anno, sono la norma piuttosto che l’eccezione. Lunghe lungaggini di carriera e alta attività sono considerate esponenzialmente rare, a suggerire una scarsità di risorse nel mondo degli attori. Questi risultati sono in accordo con le prove raccolte in precedenza, evidenziando il fatto che i tassi di disoccupazione negli attori oscillano attorno al 90% e che addirittura il 2% degli attori è in grado di guadagnarsi da vivere 24. Osserviamo anche che questa drammatica scarsità si applica in modo non equo agli attori e alle attrici, fornendo prove convincenti del pregiudizio di genere. Inoltre, si scopre che la produttività totale della carriera di un attore è distribuita sulla legge di potere, con la maggior parte degli attori che hanno pochissimi posti di lavoro, mentre alcuni di loro ne hanno più di cento. Ciò indica un meccanismo ricchissimo che sostiene la dinamica degli incarichi di lavoro, con risorse già scarse che vengono allocate in modo eterogeneo. Tutto ciò suggerisce che, mentre l’attività e la produttività sostenuta sono per definizione misure della performance 25dovrebbero, in questo contesto, essere considerati come una proxy per il successo. Solo pochi eletti saranno premiati con un Oscar, o avranno le mani sulla fama, ma questo non è importante per la maggior parte degli attori e attrici che vogliono semplicemente guadagnarsi da vivere. È la continua capacità di lavorare (al contrario del prestigio) che è più probabile che garantisca una carriera stabile. Per questi motivi proponiamo che le previsioni di successo nel mondo dello spettacolo debbano concentrarsi sull’attività e sulla produttività. Osservare a questo punto che le prestazioni sono generalmente fuse con successo 25. Mentre la performance è oggettivamente misurata in termini di azioni di un individuo, ed è tipicamente limitata, il successo è tradizionalmente misurato dal riconoscimento, cioè in termini di impatto, ed è un fenomeno collettivo che non ha limiti. Nonostante ciò, la grave scarsità di risorse nello show business ci costringe a ridefinire il successo di un attore, non in termini di popolarità o impatto, ma in termini di attività e produttività come discusso sopra. Per inciso, si noti anche che l’accreditamento su IMDb è in certa misura incanalato da meccanismi di riconoscimento come la popolarità: un produttore potrebbe offrire il lavoro all’attore che ha avuto il miglior audition o a chi ha più follower su Instagram, quindi la produttività è non solo, in senso stretto, un indicatore guidato dalle prestazioni.

Motivati ​​da questi risultati, affrontiamo quindi le domande che interessano la maggior parte degli attori e attrici che lavorano. Domande come “ho intenzione di ottenere un altro lavoro retribuito?” O “quest’anno sarà il mio migliore?”. Per prima cosa dimostriamo che l’efficienza, definita come il rapporto tra il numero totale di anni attivi e la lunghezza della carriera, è imprevedibile, in quanto non esiste una correlazione evidente tra queste due cose. Questo è in linea con studi recenti 1sottolineando che i lavori di maggior impatto nelle discipline scientifiche hanno la stessa probabilità di trovarsi in qualsiasi posizione per l’intera produzione di un individuo, e quindi non è prevedibile. Tuttavia, sorprendentemente, qui troviamo tratti distintivi nella loro disposizione temporale. In particolare, scopriamo che le carriere degli attori sono raggruppate in periodi di alta attività (striature calde) 11combinato con periodi di latenza (strisce fredde). Inoltre, scopriamo che l’anno più produttivo (annus mirabilis) sia per attori che per attrici è situato all’inizio della loro carriera e che ci sono chiari segnali che precedono e seguono la posizione dell’annus mirabilis di un individuo. Complessivamente, questi risultati inattesi ci portano a concludere che la previsione è possibile in teoria. Infine, convalidiamo questa ipotesi costruendo un modello di apprendimento statistico che predice la posizione dell’anno più produttivo, scoprendo che possiamo, con una precisione fino all’85%, dire se la carriera di un attore ha raggiunto o meno l’anno più produttivo.

risultati
Preliminari
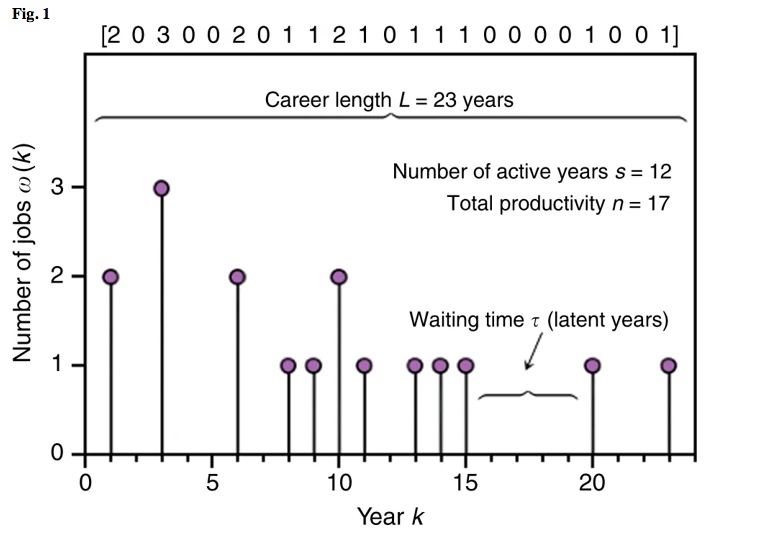
Studiamo le carriere di 1.512.472 attori e 896.029 attrici registrate su IMDb dal 16 gennaio 2016, comprese le carriere che risalgono al primo film registrato nel 1888. La carriera di ogni attore a è caratterizzata dal suo curriculum, che consiste di un insieme di coppie di numeri che rappresentano rispettivamente ogni anno in cui l’attore a è stato accreditato in IMDb, e il numero di crediti diversi in quell’anno. Come crediti contiamo il numero di lavori di recitazione in film e / o serie TV. Uno schizzo del tipico modello di attività di un attore è riportato in Fig. 1, mostrando i crediti annuali dal primo all’ultimo anno di carriera. Si noti che non ci sono solo anni attivi, in cui l’attore ha accreditato lavori in IMDb, ma anche anni latenti senza lavori registrati. Quindi riempiamo gli anni latenti con zeri e costruiamo la sequenza profilo di ciascun attore a come raffigurato nella parte superiore di Fig. 1 . La quantità w k indica la produttività locale dell’attore nell’anno k , cioè il numero di lavori accreditati in quell’anno. La lunghezza della carriera di un attore è definito come il numero di anni tra il primo e l’ultimo anno attiva (compreso), ed è indicata come L . Il numero totale di anni attivi s{𝑤𝑘}𝐿𝑘=1è da ora in poi indicato come l’attività di un attore. Poiché una carriera può avere anni latenti intrecciati con quelli attivi, dobbiamo avere s  ≤  L , inoltre L  -  s è il numero di anni latenti. Per definizione abbiamo: (i) L  ≥ 1, (ii) s  ≥ 1 e (iii) s = 1  ⇔  L = 1.

Fig. 1
Figura 1
Modello di attività professionale di un attore. La produttività annuale di un determinato attore, misurata come il numero totale di lavori pubblicati da IMDb in ciascun anno, è segnalata dal primo all’ultimo anno dell’attività dell’attore. Indicato è il caso di un attore la cui carriera ha attraversato L = 23 anni e che è stato accreditato un cumulato n = 17 lavori diversi in s = 12 anni. Dalla produttività annuale possiamo costruire la sequenza profilo attore w k , con k = 1, …, L , mostrato tra parentesi sopra il grafico, che può essere modellato come un processo punto marcato stocastico

Immagine a dimensione intera
Infine, definiamo la produttività totale n di un attore, come il numero cumulato di lavori accreditati, . L’annus mirabilis (AM) di un determinato attore è definito come l’anno in cui l’attore è stato accreditato il maggior numero di opere in IMDb: AM = m , dove m è tale che . Nel caso in cui questo m non sia univoco, prendiamo la finale in tale anno: AM = max { m }.𝑛=∑𝐿𝑘=1𝑤𝑘𝑤𝑚=max{𝑤𝑘}𝐿𝑘=1

Lunghezze di carriera e meraviglie uniche
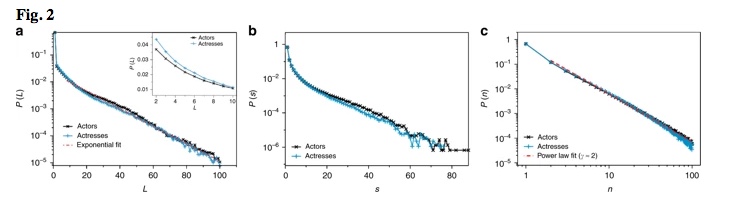
Iniziamo la nostra analisi esplorando le statistiche della durata della carriera L . In Fig. 2 a tracciamo in scala semi-registro la distribuzione empirica delle lunghezze di carriera P ( L ), sia per gli attori che per le attrici che trovano che la coda è ben adattata da una distribuzione esponenziale. Per costruzione, P ( L = 1) = P ( s= 1) e questa quantità rappresenta la percentuale di prodigi one-hit, ovvero di attori la cui carriera è iniziata e finita, secondo IMDb, nello stesso anno. È interessante notare che la percentuale di questi casi è estremamente elevata (circa il 69% per i maschi e il 68% per le donne) e si discosta dalla distribuzione esponenziale altrimenti decadente. Questa forte deviazione sottolinea che le meraviglie di un solo colpo non sono un’eccezione nel mondo dello spettacolo, ma, al contrario, sono la norma 26 . Uno zoom della distribuzione nell’intervallo L ∈[2, 10] è riportato nell’inserto di (a), rivelando differenze sistematiche tra attori e attrici, suggerendo che è sempre più comune trovare attrici (non di successo) con carriere più brevi degli attori. Abbiamo effettivamente eseguito un esperimento di selezione del modello che conferma che il pregiudizio di genere è statisticamente significativo (vedere la nota integrativa 1 per i dettagli).

Fig. 2
figura 2
Lunghezza della carriera, distribuzione dell’attività e produttività. a La probabilità P ( L ) che un attore o un’attrice abbia una carriera di lunghezza L , stimata calcolando l’istogramma di frequenza del numero di anni tra la prima e l’ultima voce registrata su IMDb. P (1) misura l’abbondanza di “prodigi one-hit”, ovvero attori o attrici con record IMDB in un solo anno. Uno zoom per L ∈ [2, 10] nell’inset mostra che le carriere che vanno da 2 a 10 anni sono proporzionalmente più frequenti nelle donne che negli uomini. b Distribuzione dell’attività P ( s) stimata calcolando l’istogramma di frequenza del numero di anni di lavoro all’interno di ciascuna carriera ( s  ≤  L ). Le curve per attori e attrici sono molto simili ed entrambe mostrano una chiara coda esponenziale, che implica una “scarsità di risorse”. c Grafico del logaritmo delle distribuzioni di produttività totali P ( n ) per attori (neri) e attrici (blu). Entrambe le curve si decompongono come una legge di potenza P ( n ) ~ n -γ , dove γ  ≈ 2, rivelando la legge di Zipf per il numero totale di lavori di recitazione

Immagine a dimensione intera
La distribuzione di probabilità empirica di attività, visualizzando la probabilità di campionamento un attore che ha lavorato in s anni, è mostrato in Fig. 2b in una scala semi-log. La maggior parte degli attori e attrici sono attivi solo in un anno ( s = 1), come per impostazione predefinita . La probabilità di trovare attori con una grande attività, cioè quelli che hanno lavorato in molti anni diversi, decade esponenzialmente velocemente. Questo decadimento esponenziale imita il decadimento simile nella probabilità di trovare lunghe lunghezze di carriera e complessivamente sono la base per rivendicare una scarsità di risorse nel mondo dello spettacolo, cioè ci sono molti più attori / attrici che offerte di lavoro 27𝑠=1↦𝐿=1. Questa mancanza di risorse porta naturalmente a una domanda: come sono allocati? Affrontiamo questa domanda nella prossima sezione.

Produttività e fenomeno ricco di ricchezze
La figura 2c mostra le distribuzioni empiriche della produttività totale P ( n ), riportando i numeri normalizzati di attori o attrici con n apparizioni in film o serie TV durante la loro carriera. Mentre la distribuzione di lunghezza carriera P ( L ) e le distribuzioni di attività P ( s ) sono ben adattate nelle loro code da una legge esponenziale, la funzione P ( n ) decade più lentamente e può essere adattata da una legge di potenza P ( n ) ~  n – γ con esponente γ ≈ 2. Si noti che comportamenti simili sono già stati trovati nel contesto di reti attore-film in due modalità e di altri sistemi che possono essere modellati come grafici bipartiti 28 . Una legge di potenza nella distribuzione della produttività totale implica anche l’esistenza di un ridimensionamento nella distribuzione della produttività di rango-frequenza. È infatti ben noto che osservare una distribuzione di legge di potenza con esponente γ per l’abbondanza di alcune variabili equivale a ottenere un ridimensionamento della legge di potenza per la frequenza della variabile che appare con rank r : f ( r ) ~  r – α 29 . Gli esponenti delle due leggi di ridimensionamento sono matematicamente correlati tramite α= 1 / ( γ  - 1). La celebre legge di Zipf fa riferimento al caso particolare di un esponente α  ≈ 1, che è proprio il caso qui. A sua volta, l’emergere della legge di Zipf per la distribuzione della frequenza di rango della produttività totale di un attore suggerisce una possibile spiegazione meccanicistica per le nostre osservazioni. Molte diverse proposte per il meccanismo alla base dell’emergere della legge di Zipf, e diversi nomi per il fenomeno stesso, sono state presentate in vari contesti, tra cui il processo Simon-Yule, il meccanismo di attaccamento preferenziale, l’effetto Matthew, il principio di Gibrat , ricco diventa più ricco, ecc.

In questo contesto, possiamo suggerire un possibile meccanismo per l’inizio di una distribuzione della legge di potenza per la produttività totale in termini di un fenomeno ricchissimo. Consideriamo un modello generativo di un grafico bipartito i cui due gruppi di nodi rappresentano rispettivamente attori e film. Gli attori acquisiscono nuovi collegamenti ai film, aumentando così la loro produttività, se ottengono un ruolo in quei film. Supponiamo che tutti i nodi dell’attore inizino con zero bordi e acquisiscano i loro primi archi solo in base ad una forma fisica, che viene inizialmente assegnata a caso o su qualche ipotetica abilità di recitazione intrinseca. Quando più nodi del film entrano nella rete, i nodi attori che acquisiscono nuovi margini guadagnano popolarità e questo, a sua volta, aumenta la loro forma fisica. Come è noto, i produttori sono più desiderosi di offrire un ruolo agli attori popolari, i nodi dell’attore con alta idoneità hanno maggiori probabilità di attirare nuovi margini. Ciò porta a un effetto moltiplicativo che esprime chiaramente il fenomeno ricco di ricchezze; gli attori con molti incarichi di lavoro avranno una maggiore possibilità di lavorare anche più degli attori con bassa produttività. In conclusione, lo stesso meccanismo ricco di ricchezze, che è al centro delle reti con distribuzioni di laurea in legge di potere30 , 31 , 32 , 33 , possono anche essere la causa delle leggi di potenza osservate nella produttività totale degli attori cinematografici. Questo risultato non è affatto inaspettato, dopotutto, il più noto è un attore, più è probabile che i produttori lo desiderino nel loro prossimo film, se non altro per scopi commerciali. Ciò che forse è drammatico in questa osservazione è che è risaputo che gli effetti ricchi di ricchezze sono piuttosto arbitrari e imprevedibili, poiché i grandi hub possono evolversi da fluttuazioni iniziali imprevedibili e casuali che sono state amplificate e non basate su alcun particolare intrinseco fitness 33(come le abilità di recitazione). Citando Easly e Kleinberg: “se potessimo tornare indietro di 15 anni e poi ricominciare la storia, i libri di Harry Potter venderanno ancora centinaia di milioni di copie, o languirebbero nell’oscurità mentre alcuni altri lavori di fantascienza per bambini hanno ottenuto importanti risultati successo?”. È un dato di fatto, sembra probabile che attraverso diversi universi paralleli la produttività disporrebbe ancora di una distribuzione della legge di potenza, ma è tutt’altro che chiaro che gli attori più produttivi sarebbero sempre gli stessi. È interessante notare che quest’ipotesi è stata recentemente convalidata in un esperimento sociale online per il caso della popolarità musicale 34 . In sintesi, la produttività è probabilmente la variabile che ogni attore punta a massimizzare, ma questi risultati suggeriscono che l’aumento della produttività può essere più un effetto di rete35 , 36 che una conseguenza delle capacità di recitazione.

L’efficienza è imprevedibile
In Fig. 2 abbiamo osservato che la lunghezza della carriera L e l’attività s sono variabili che sono entrambe distribuite in modo esponenziale, indicando una scarsità di risorse. In questa sezione esploreremo ulteriormente se le due quantità L e s sono correlate. Per prima cosa definiamo l’efficienza di un attore come il rapporto s / l degli anni attivi sull’intera carriera e indaghiamo su come viene distribuita l’efficienza. I risultati riportati in Figura 1 supplementare , mostrano che: (i) la distribuzione dell’efficienza diminuisce rapidamente come s / Lsi avvicina a zero o a uno, la maggior parte degli attori e delle attrici ha valori intermedi di efficienza e (2) per l’efficienza a medio raggio la distribuzione è essenzialmente uniforme (si veda la nota integrativa 2 per ulteriori dettagli). Questo suggerisce che l’efficienza non è prevedibile e che, per l’efficienza di gamma media, gli unici correlazioni che emergono tra l’attività s e la lunghezza carriera L derivano dal fatto che, per costruzione, s  ≤  L . Per convalidare ulteriormente questo, abbiamo eseguito un diagramma a dispersione di s contro Lper tutti gli attori e le attrici e calcolato il coefficiente di correlazione di Pearson, quindi confrontato con il coefficiente di correlazione di un modello nullo generato estraendo a caso valori di L e s dal pool di profili di carriera, assicurando che L  ≥  s (Supplementare Fig. 2 ). Per gli attori, s e L mostrano un coefficiente di correlazione di Pearson r  ≈ 0,69, mentre nel modello nullo abbiamo ottenuto r nulla  ≈ 0,6. Nel caso di attrici abbiamo trovato r  ≈ 0.69 and r null  ≈ 0.58. Come previsto, s e Lsono infatti quantità correlate, ma le correlazioni possono essere quasi interamente spiegate da un modello nullo. In altre parole, per intervalli intermedi non ci sono ulteriori correlazioni tra lunghezza e attività: l’attività degli attori non può quindi essere prevista dalla loro lunghezza di carriera, e possiamo concludere che l’efficienza è una quantità imprevedibile.

Le carriere degli attori sono raggruppate in striature calde e fredde
Per comprendere la disposizione temporale degli anni attivi all’interno della sequenza profilo di un determinato attore, ora consideriamo le statistiche dei tempi di attesa. Un tempo di attesa τ è definito come il tempo trascorso (in anni) tra due anni attivi (equivalentemente, un tempo di attesa è una raccolta di anni latenti successivi), e le sue statistiche forniscono un modo classico per analizzare la presenza di memoria e scoppi nel tempo serie 37 , 38 . Abbiamo stimato la distribuzione P ( τ ) dei tempi di attesa per attori e attrici, scartando quelli con brevi lunghezze di carriera, L<10 anni, per evitare una mancanza di statistiche. Per stimare questa distribuzione, per ogni attore (attrice) contiamo quanto frequentemente si osservano i tempi di attesa di una certa durata τ e si normalizzano le frequenze accumulate. Questo processo introdurrà inevitabilmente pregiudizi di dimensioni finite poiché, per brevi periodi di carriera, è più probabile trovare tempi di attesa brevi, semplicemente perché non c’è spazio per quelli lunghi. Per un corretto confronto abbiamo quindi calcolato anche la distribuzione per un modello null randomizzato P null ( τ ) in cui tutte le sequenze del profilo sono state mescolate (mantenendo il primo evento w 1 e l’ultimo evento w Linalterato). Una mancanza di correlazioni temporali implicherebbe P null ( τ ) = P ( τ ), mentre le differenze sistematiche suggeriscono l’insorgenza di correlazioni temporali nell’attività degli attori. Nel pannello (a) di Fig. 3 riportiamo la differenza P ( τ ) -  P nullo ( τ ) in funzione di τ .

Fig. 3
Figura 3
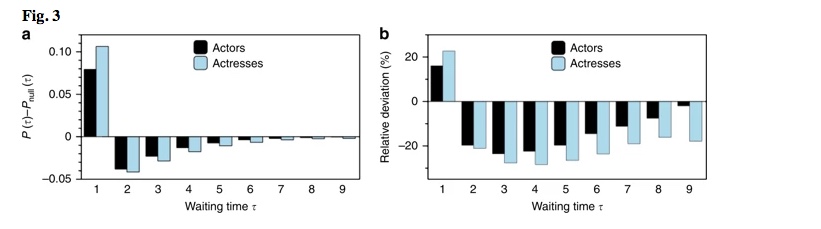
Distribuzione del tempo di attesa. a Differenza P ( τ ) -  P nullo ( τ ) tra la distribuzione del tempo di attesa nelle sequenze del profilo e in un modello nullo randomizzato, per attori (barre nere) e attrici (barre blu). I tempi di attesa sistematicamente brevi, τ  = 1, sono sovrarappresentati rispetto al modello null, mentre il contrario è vero per i tempi di attesa intermedi τ > 1. b La differenza relativa percentuale [ P ( τ ) -  P null ( τ )]  ⋅  100 / P null ( τ) rivela una notevole differenza tra attori e attrici: le strisce fredde svaniscono più velocemente per gli attori

Immagine a dimensione intera
Per entrambi gli attori e le attrici, troviamo sistematicamente P nullo ( τ = 1) < P ( τ = 1) e P nullo ( τ > 1)> P (τ> 1), cioè gli anni attivi sono più raggruppati di sarebbe per caso, e quindi lo stesso è vero per periodi di inattività. Ciò significa che la sequenza profilo mostra clustering ed è composta da raffiche di attività (hot streaks) in cui attori e attrici sono più propensi, di quanto ci si aspetterebbe per caso, a lavorare in un anno se hanno lavorato l’anno prima ( τ = 1) . Questo risultato è in accordo con le recenti scoperte in altri lavori creativi nella scienza e nell’arte 11. Inoltre, queste strisce calde sono intervallate da periodi di latenza anormalmente lunghi (strisce fredde) in cui gli autori sono meno probabili di quelli casuali a lavorare in un dato anno se non hanno funzionato l’anno prima ( τ > 1).

Inoltre, per confrontare opportunamente le deviazioni dal modello nulla per diversi tempi di attesa, in Fig. 3 b tracciamo la differenza relativa (in percentuale) [ P ( τ ) -  P nullo ( τ )] · 100 / P nullo ( τ ). Troviamo una sostanziale differenza tra attori e attrici: mentre la deviazione dal modello null decade per i tempi di attesa più grandi τ nel caso degli attori, per le attrici viene mantenuta questa deviazione relativa, indicando un kernel di memoria più lungo, a sua volta suggerendo che avere un periodo di latenza è nel complesso più dannoso per le attrici che per gli attori.

Predire l’annus mirabilis
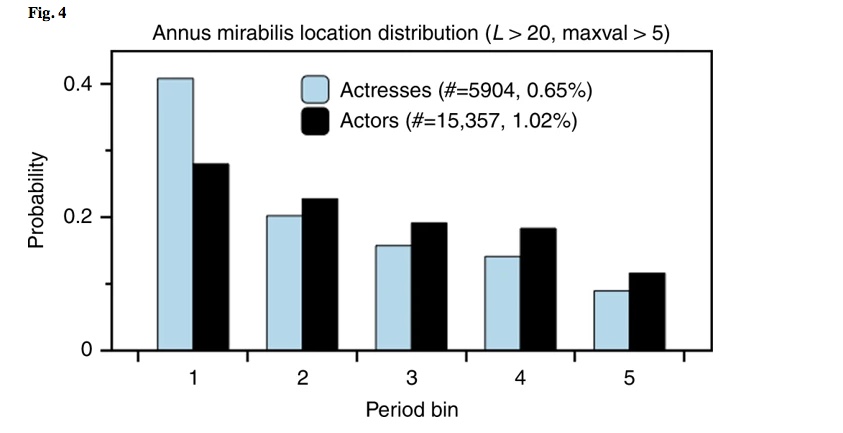
È stato recentemente scoperto che la pubblicazione più interessante che uno scienziato produrrà è altrettanto probabile che si verifichi in qualsiasi fase della loro carriera 1 . Qui esploriamo una domanda correlata nel contesto di attori e attrici. Invece di impatto, l’indicatore del successo in studio è la produttività, misurata dal numero di opere accreditate in IMDb. Ci concentriamo su attori e attrici con vite lavorative che vanno oltre L = 20 anni. Limitiamo i nostri risultati riportati a quei casi in cui vi erano almeno 5 lavori accreditati nell’annus mirabilis (AM), sebbene altre soglie producano risultati qualitativamente simili. Il sottoinsieme di attori con L> 20 e più di 5 lavori di recitazione nell’AM sono composti da 15357 attori (1,02%) e 5904 attrici (0,65%). L’ampia differenza di genere indica che gli attori tendono ad avere più posti di recitazione rispetto alle attrici.

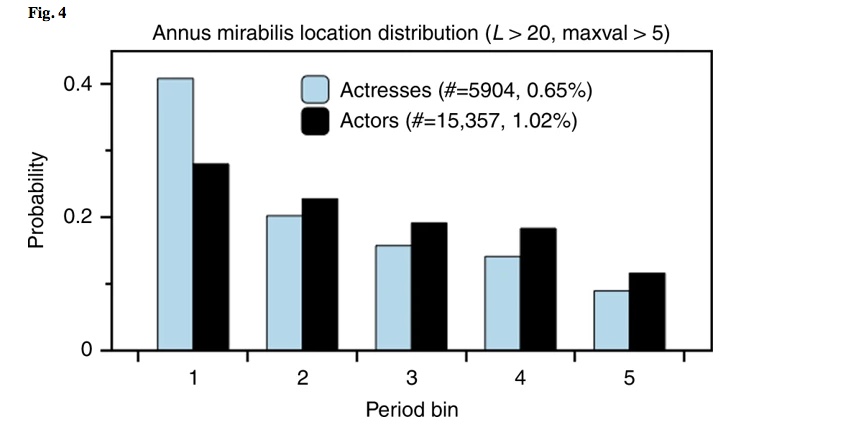
In Fig. 4 tracciamo la probabilità con cui l’AM si verificherà in ogni punto della carriera di un attore o attrice. Per poter confrontare queste probabilità su carriere di lunghezza variabile, abbiamo suddiviso rispettivamente le serie storiche di L degli attori in 5 bin (le altre segmentazioni producono risultati qualitativamente simili). Le trame indicano costantemente che la posizione più probabile dell’annus mirabilis è verso l’inizio di una carriera. Sebbene i risultati siano qualitativamente simili per attori maschili e femminili, questo pregiudizio è molto più pronunciato nel caso delle attrici, confermando ulteriormente la differenza di genere precedentemente osservata.

Fig. 4
Figura4
Annus mirabilis tende a verificarsi prima piuttosto che dopo. Posizione di AM all’interno della carriera di un attore o attrice, in cui la lunghezza della carriera viene scomposta in 5 contenitori in ogni caso, per poter confrontare i profili di diverse lunghezze di carriera. Troviamo sistematicamente che la posizione più probabile dell’annus mirabilis è verso l’inizio di una carriera, anche se questo effetto è considerevolmente più acuto nel caso delle attrici

Immagine a dimensione intera
Per studiare se è possibile rilevare l’apparizione imminente di annus mirabilis di un attore, abbiamo analizzato, per attori e attrici, il numero medio di lavori di recitazione prima e dopo l’AM. Per fare ciò in modo coerente, inizialmente eseguiamo una traduzione che allinea tutte le sequenze del profilo, in modo che l’annus mirabilis k = y * si verifichi tutti a κ = 0. Quindi definiamo :𝑘↦κ

ξ( κ) = 1| 𝐴 |Σ𝑖 = 1| 𝐴 |𝑤( 𝑖 )𝑦*+ κ,
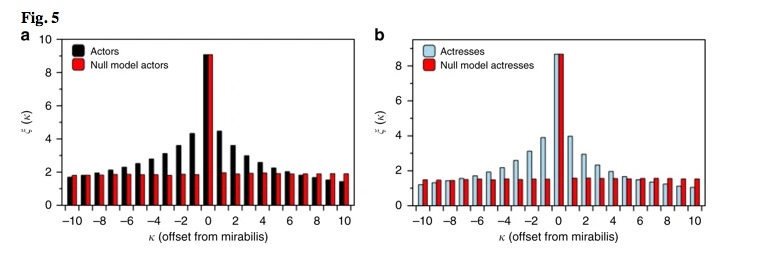
dove κ è lo scostamento dall’annus mirabilis e | A | è la dimensione dell’insieme di attori / attrici per i quali esiste una sequenza profilo con un input all’offset κ . In Fig. 5 tracciamo ξ ( κ ), mostrando che, in media, c’è un netto aumento del numero di lavori che precedono l’AM e una chiara diminuzione immediatamente successiva. Questo modello è assente nei corrispondenti modelli nulli ottenuti mischiando le sequenze del profilo (barre rosse).

Fig. 5
Figure5
L’annus mirabilis è prevedibile. Il numero totale di lavori che agiscono, ξ ( κ ), come media di tutti a attori e b attrici, viene riportato in funzione del numero di anni κ prima o dopo le mirabilis. Solo attori e attrici con una carriera che dura più di L = 20 anni e annus mirabilis con w lavori> 5 recitazione sono stati selezionati. In entrambi i casi, osserviamo un chiaro schema non monotono, che indica che l’annus mirabilis si sta avvicinando o è appena passato. Per confronto, riportiamo in rosso i risultati ottenuti per un modello nullo in cui le sequenze di profilo di tutti gli attori e attrici sono state mescolate. In questo caso non emerge alcun modello

Immagine a dimensione intera
È interessante notare che modelli simili sono stati osservati prima nel contesto della produttività scientifica, sebbene la recente ricerca metta in discussione questo paradigma 23 . In effetti, in 23 gli autori hanno sfruttato le forme osservate dei profili di produttività scientifica e hanno seguito un approccio di apprendimento non supervisionato per raggruppare diversi tipi di carriere. Qui, invece, seguiremo un approccio di apprendimento supervisionato e ora mostreremo come i pattern osservati possono essere effettivamente sfruttati per costruire un metodo per la previsione anticipata dell’annus mirabilis.

Sulla base della nostra distribuzione osservata di lavori che circondano l’annus mirabilis, inizialmente proponiamo un criterio di allerta precoce: se la sequenza di carriera è non monotona attorno al valore di k , cioè, se w k > w k -1 e w k +1 < w k , quindi l’anno k è un buon candidato per l’annus mirabilis. Con questo criterio in mente, si potrebbe porre la seguente domanda: dato un esempio di sequenza di profilo di un attore o attrice, possiamo dire se l’annus mirabilis è già passato o no? Matematicamente, la domanda di cui sopra può essere formalizzata come segue: data una sequenza di carriera( 𝑤𝑘)𝐿𝑘 = 1in modo tale che la massima produttività totale si verifichi al tempo k = y * , si consideri una sequenza troncata . Ora desideriamo sapere se possiamo valutare con precisione se y * ∈  {1, …, T } usando solo . Questo forma un problema di classificazione binaria, in cui se e altrimenti. Il nostro criterio ingenuo, come illustrato sopra, fornisce prontamente l’euristica: se è monotono e𝑤¯𝑘= ( 𝑤𝑘)𝑇≤ 𝐿𝑘 = 1 𝑤¯𝑘𝑤¯𝑘∈ 1𝑦*∉{ 1 , . . . , 𝑇}𝑤¯𝑘∈ 2𝑤¯𝑘∈ 1𝑤¯𝑘𝑤¯𝑘∈ 2 se non. Quando questo metodo viene testato su un set opportunamente generato di sequenze troncate (vedere la nota supplementare 3 per i dettagli), troviamo che è corretto ~ 69,2% delle volte per gli attori e ~ 75,0% delle volte per attrici. Questo modello ora costituisce un punto di riferimento rispetto al quale testeremo un approccio più raffinato. L’idea è di rilassare il nostro metodo di classificazione introducendo alcuni parametri che consentono di deviare dall’euristica rigida, quindi di addestrare quei parametri su qualche sottoinsieme , e successivamente testare l’addestramento modello sul set di prova . Per fare questo, prima definiamo la funzione⊊ ∖ 

𝐷 ( 𝑤¯𝑘) = – Σ𝑦 = 1𝑇- 1m i n (0, 𝑤¯𝑦 + 1- 𝑤¯𝑦) .
(1)
Ad ogni anno k il contributo a D di quell’anno è zero se la produttività totale nell’anno successivo è maggiore. Ciò significa che per una sequenza monotonicamente crescente , . Se la produttività diminuisce dall’anno k a k + 1, allora D aumenterà di un importo corrispondente.𝑤¯𝑘𝐷 ( 𝑤¯𝑘) = 0

𝐷 ( 𝑤¯𝑘) misura in modo efficace la distanza dall’aumentare monotonicamente, quindi possiamo usarlo per rilassare la nostra euristica ingenua definendo una soglia d tale che la regola di decisione diventa𝑤¯𝑘𝐶( 𝑤¯𝑘, 𝑑 )

𝐶( 𝑤¯𝑘, 𝑑 )= { 12io f𝐷 ( 𝑤¯𝑘)<𝑑io f𝐷 ( 𝑤¯𝑘) ≥ 𝑑 .
(2)
Questo nuovo classificatore è più flessibile dell’euristica ingenua in quanto abbiamo introdotto un parametro d che ora può essere ottimizzato (addestrato) come segue: se denotiamo come la vera classe della sequenza , quindi il valore ottimale del parametro d * è il valore di d che minimizza la seguente funzione di perdita𝐶*( 𝑤¯𝑘)𝑤¯𝑘

 ( , 𝑑 ) =- Σδ ( 𝐶( 𝑤¯𝑘, 𝑑 ), 𝐶*( 𝑤¯𝑘) ).
(3)
Dove δ ( X , Y ) produce uno se X = Y e 0 altrimenti. Questo valore per d * viene quindi utilizzato per classificare le sequenze rimanenti in . I risultati di questi test su attori e attrici possono essere parzialmente riassunti dalle due matrici di confusione CO m (per attori) e CO f (per attrici):∖ 

C O𝑚= [ 3377510771565952000] ,C O𝑓= [ 125493596259326682]
(4)
Le metriche classiche utilizzate per valutare le prestazioni del classificatore, ovvero precisione, precisione, richiamo e punteggio F1, sono riassunte nella Tabella 1 . Scopriamo che l’accuratezza della previsione è rispettivamente dell’84% e dell’86%, cioè ~ 10% in più rispetto a quelle ottenute usando un’euristica ingenua.

Tabella 1 Metriche delle prestazioni (accuratezza, precisione, richiamo e punteggio F1) del metodo di classificazione proposto per la previsione del mirabilis annus
Tavolo full size
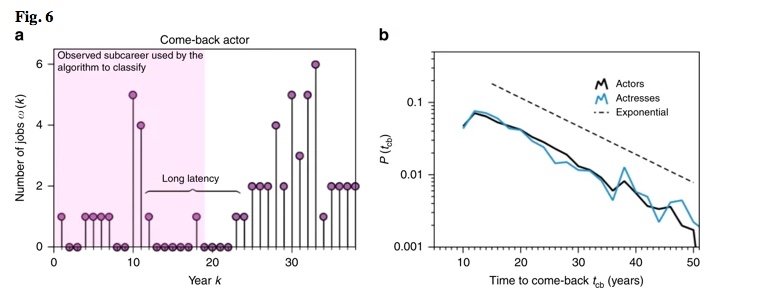
Per concludere, abbiamo esplorato ulteriormente la natura del ≈15% dei campioni che sono classificati in modo errato (vedere la nota supplementare 3 per i dettagli). Abbiamo scoperto che i falsi negativi (campioni per i quali l’annus mirabilis è ingiustamente previsto che deve ancora venire) sorgono a causa della natura conservativa del modello di predizione, quindi versioni più raffinate del modello di predizione potrebbero produrre risultati di previsione ancora migliori (Fig. . 3 ). Viceversa, scopriamo che i falsi positivi – dove l’annus mirabilis è erroneamente predetto che siano passati – sono di solito legati a attori e attrici che stanno vivendo un ritorno in una fase successiva della loro carriera (vedi Fig. 6a) . per un esempio). È interessante notare che le posizioni di queste ultime esplosioni di attività sembrano essere fondamentalmente difficili da prevedere (Fig. 6b ).

Fig. 6
figure6
I comeback degli attori sono imprevedibili. una sequenza tipica di profilo di un attore che esibisce un ritorno dopo un lungo periodo di latenza. Tali casi potrebbero portare a classificazioni errate quando il subcareer alimentato all’algoritmo di predizione (evidenziato in rosa) cattura un lungo periodo di latenza: l’algoritmo di predizione classifica erroneamente la sequenza rosa come quella in cui l’annus mirabilis ha superato. b Distribuzione semi-log di probabilità del lasso di tempo stimato dal (erroneamente stimato) annus mirabilis a quello vero (cioè il tempo t cbper tornare agli attori con sequenze di profili come quella nel pannello a), per quei campioni misclassificati in cui l’algoritmo predice erroneamente che l’annus mirabilis era già passato (un binning lineare è stato applicato ai dati). Modellando la posizione del picco secondario (comeback burst) come variabile casuale, il fatto che P ( t cb ) decada in modo esponenziale, suggerisce che questa variabile casuale è senza memoria (processo di Poisson), vale a dire, il burst di ritorno è intrinsecamente imprevedibile

Immagine a dimensione intera
Discussione
In questo lavoro abbiamo fatto uso della grande quantità di dati presentati da IMDb per esplorare, analizzare e prevedere il successo sul grande schermo. Studiando le carriere di 1.512.472 attori e 896.029 attrici dal 1888 fino al 2016, abbiamo scoperto una serie di modelli distintivi che includono una scarsità endemica di risorse, un meccanismo ricco di ricchezze nell’assegnazione del lavoro, l’inizio di striature calde e fredde. di produttività 11 e un annus mirabilis che può effettivamente essere previsto. Tali modelli – che mostriamo differiscono sistematicamente per attori e attrici, suggerendo forti prove di pregiudizi sessuali 26 – non solo ci permettono di identificare le qualità dei singoli attori o delle attrici che lavorano vite, ma anche di ottenere una visione più profonda dei meccanismi con cui vengono assegnati i posti di lavoro, dove l’alta produttività non è necessariamente basata sul merito ed è probabile che sia un effetto di rete 34 , 35 , 36 . Sulla base delle nostre scoperte, abbiamo quindi costruito un modello di apprendimento statistico che prevede fino all’85% di accuratezza se un attore o un’attrice avrà probabilmente un futuro migliore, o se i giorni migliori sono, sfortunatamente, alle spalle. Mentre ci aspettiamo che le versioni perfezionate del modello di predizione forniscano un’accuratezza ancora maggiore, vale la pena notare che gli attori con lunghi periodi di latenza che poi subiscono ritorni tardivi sono rari ma intrinsecamente difficili da prevedere.

Speriamo che i metodi presentati e i risultati ottenuti contribuiranno alla nuova scienza del successo 35 . Dato lo scopo delle nostre scoperte in tutto il settore, vorremmo anche che il nostro articolo fosse di interesse per coloro che lavorano nel mondo dello spettacolo.

Disponibilità dei dati
I dati sono disponibili su richiesta o accessibili all’indirizzo https://doi.org/10.17605/OSF.IO/NDTA3

Disponibilità del codice
I codici sono disponibili su richiesta.

I